이번글에서는 중심극한 정리를 소개합니다.
저번글에서는 $[0,1]$ 구간에서 uniform random 변수를 생성하는 여러 가지 방법을 알아봤는데, 사실 정규분포를 따르는 난수를 발생하는 데에 궁극적인 목적이 있습니다. 그 과정에서 알아두는 좋을 것이 바로 중심극한정리입니다.
어떤 $n$개의 확률변수(또는 샘플) $X_1, X_2, \cdots, X_n$ 있고, 이것들이 다 동일한 분포를 따르고 서로 독립이라 합시다(이것을 iid, independent and identically distributed, 독립 항등 분포라고 다양하게 부릅니다.)
$X_i$ 각각의 평균은 $\mu$, 분산을 $\sigma^2$이라 합시다. 이들의 표본 평균 $\bar{X}$을
$$\bar{X} = \frac{X_1+X_2+\cdots+X_n}{n} =\frac1n \sum_{i=1}^n X_i \tag{1}$$
라 하면
중심극한정리(CLT, Central Limit Theorem)
$n$이 무한정 커질 때,
$$ \bar{X} \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{n} \right) $$
라는 것입니다. $\mathcal{N}$은 정규분포를 뜻합니다.
이 정리의 key point는 바로 정규분포를 따른다는 데 있습니다. 왜냐면 무작정 $\bar{X}$의 평균과 분산을 구해보면
$$\mathbb{E}(\bar{X}) = \frac1n\sum_{i=1}^n \mathbb{E}(X_i) = \frac1n \sum_{i=1}^n \mu = \mu$$
이고
$$\mathbb{V}(\bar{X}) = \frac{1}{n^2} \sum_{i=1}^n \mathbb{V}(X_i) = \frac{1}{n^2} \sum_{i=1}^n \sigma^2 = \frac{\sigma^2}n$$
입니다.
이렇게 평균, 분산은 구하기가 쉽습니다. 그런데 이게 정규분포를 따른다는 것이 획기적인 거죠. 예제를 보겠습니다.
1. 동전 던기지

1. 동전의 앞면을 0, 뒷면을 1이라 하고 몇 번 던져봅니다. 그래서 나온 sample(표본)들을 평균합니다. 이것이 표본 평균이죠.
2. 이 표본 평균들을 아주 많이 구합니다. 이 구한 것들을 히스토그램을 그려서 분포를 살펴봅니다.
3. 중심 극한 정리에 따르면, 1번에서 표본의 개수가 많을수록(수식(1)의 $n$) 정규분포로 가겠죠, 이게 맞는지 2번 그래프에서 살펴보는 겁니다.
먼저 python code를 보시죠.
import math
import numpy as np
import matplotlib.pyplot as plt
def clt_coinTest():
coin_face = [0, 1]
nAct = 20
nSimulation = 5000
data =[]
for i in range(nSimulation):
res = np.random.choice(coin_face, size=nAct)
res_avr = np.average(res)
data.append(res_avr)
plt.hist(data, bins=20)
plt.show()
if __name__ == '__main__':
clt_coinTest()
nAct = 20이 부분은 표본 평균을 만들 샘플의 갯수입니다. 일단 $n=20$이라 하죠.
nSimulation = 5000표본평균을 5000개 만드는 변수입니다
res = np.random.choice(coin_face, size=nAct)
res_avr = np.average(res)
data.append(res_avr)- 개수(size)가 nAct 개인 난수 배열을 만듭니다. coin_face 가 [0,1] 두 원소로 이루어진 list형 data이고 이 중에서 radom choice 해서 res라는 변수에 쌓는 것입니다.
- res에 쌓인 데이터들을 average 합니다. 그럼 결과적으로 res_avr이 표본 평균이 됩니다.
- 이 표본 평균을 data라는 변수에 쌓습니다.
plt.hist(data, bins=20)계급의 개수가 20개인 histogram을 만듭니다.
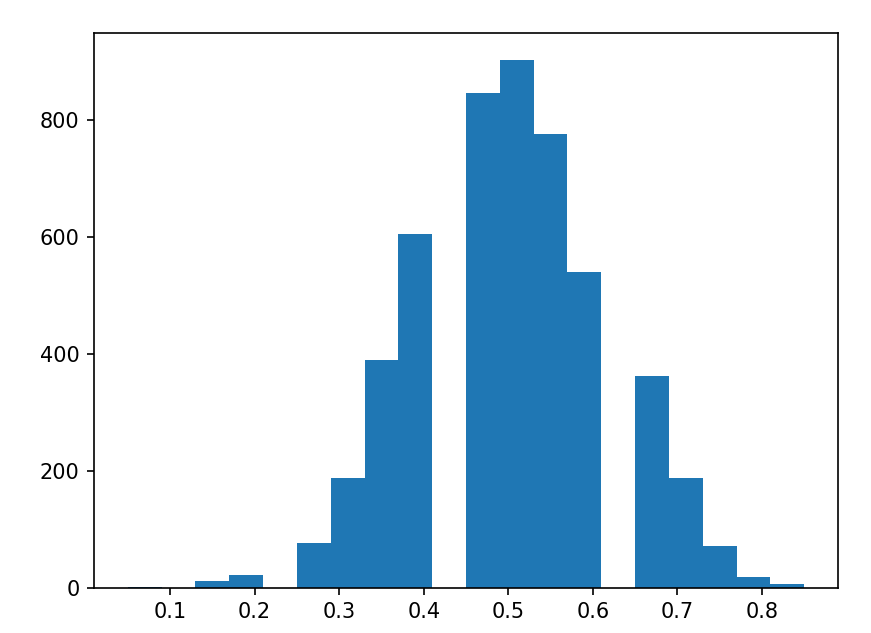
뭔가 정규분포스럽지만.. 처참한 결과이지요. 아예 데이터가 없는 이빨 빠진 구간도 보입니다. 정규분포라고 하기엔 무리가 있습니다. $n$을 크게 키워볼까요?
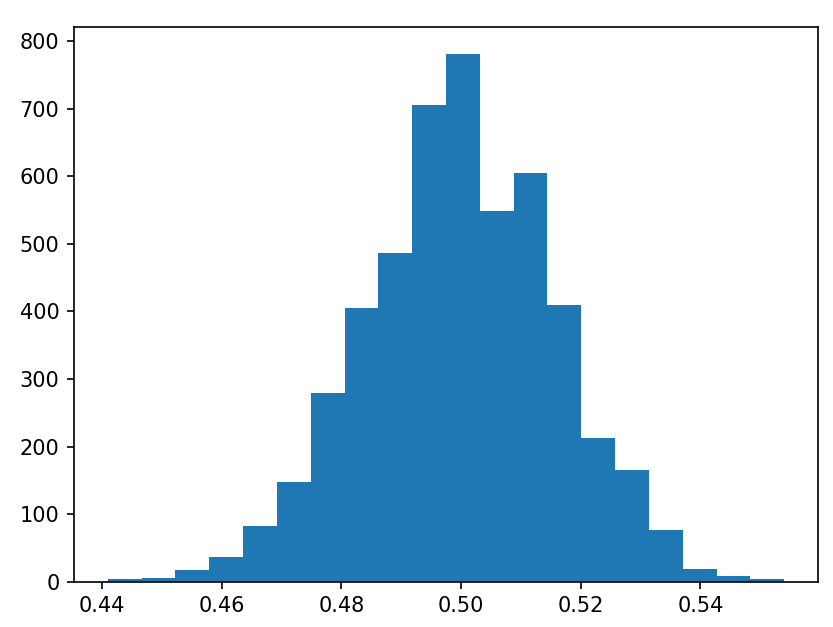
알이 속속들이 차있는 약간의 대칭형 모양이 나옵니다. $n$을 더 키워보겠습니다.

비로소 대칭형 모양이 나오는 듯합니다. 여기서 중요한 사실은 히스토그램이 그려지는 $x$축의 range를 보시죠.
$n=20$일 때는 0.1~0.8, $n=1000$일 때는 0.44~0.56 , $n=100,000$일 때는 0.495~0.595 사이로 좁아지게 되죠? 중심 극한 원리 때문입니다.
동전 던졌을 때 나오는 면이 0,1 인 확률변수 $X$의 확률은 각각 $\frac12$입니다. 즉,
| $X$ | 0 | 1 |
| $p$ | $\frac12$ | $\frac12$ |
입니다. $X$의 평균과 분산을 각각 구해보면
$$\mathbb{E}(X) = \frac12, \mathbb{V}(X)= \mathbb{E}(X^2) -(\mathbb{E}(X))^2 = 1-\frac14= \frac34$$
입니다.
따라서 표본평균 $\bar{X}$의 평균과 분산은 각각
$$\mathbb{E}(\bar{X}) = \frac12 , \mathbb{V}(\bar{X}) =\frac3{4n}$$
이 됩니다. 따라서 $n$이 커질수록, 분산이 0으로 가게 되어 히스토그램처럼 range가 줄어들게 되는 것이죠.
주사위도 던져볼까요?
2. 주사위 던지기

동전과 달리 주사위는 6개의 면이 있습니다.
python code는 다음과 같습니다. 동전 던지기 code와 거의 비슷합니다.
import math
import numpy as np
import matplotlib.pyplot as plt
def clt_diceTest():
dice_face = [1, 2, 3, 4, 5, 6]
nAct = 100000
nSimulation = 5000
data =[]
for i in range(nSimulation):
res = np.random.choice(dice_face, size=nAct)
res_avr = np.average(res)
data.append(res_avr)
plt.hist(data, bins=20)
plt.show()
if __name__ == '__main__':
clt_diceTest()결과를 볼까요? 표본 평균이 10만 인 상황입니다.
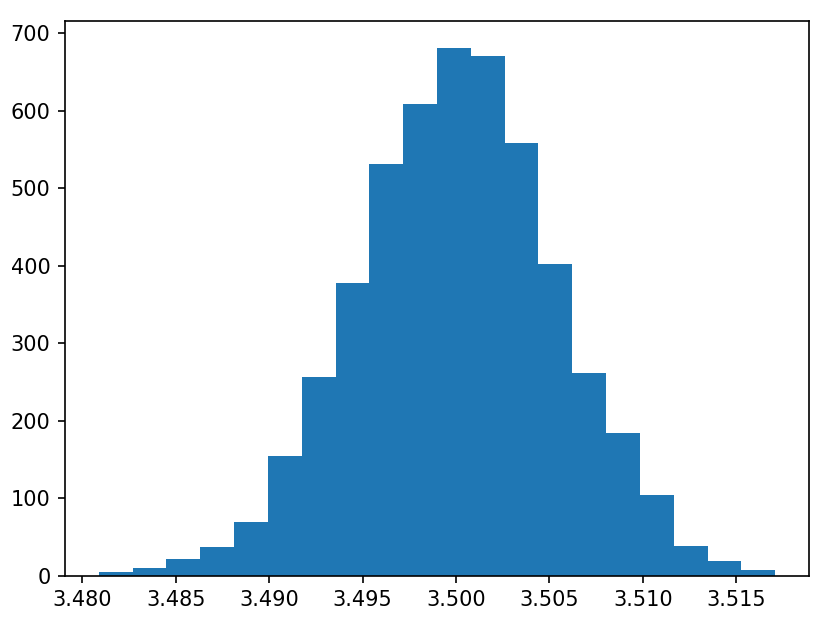
물론 이것도 $n$이 작으면 처참한 그림이 나오죠
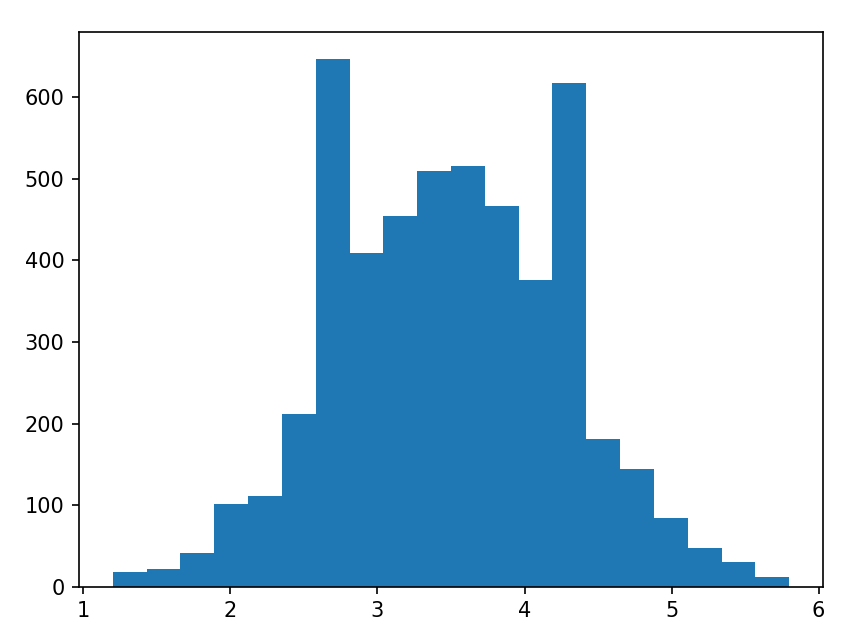
위의 예제에서 보았듯이 표본 평균의 분포는 표본이 많아질수록 정규분포 모양을 띄게 됩니다. 위의 동전, 주사위 예제는 아주 간단한 관찰이었고, 다음 글에서는 정말 제대로 된 정규분포 모양을 얻기 위해 uniform random변수들을 이용해 볼 생각입니다.

'수학의 재미 > 확률분포' 카테고리의 다른 글
| 정균분포 난수를 만들어 주세요 #2 : Normal CDF 이용 (0) | 2022.06.13 |
|---|---|
| 정균분포 난수를 만들어 주세요 #1 : 중심극한정리 이용 (0) | 2022.06.13 |
| 균등난수(uniform random number) 만들어보자 #3 : Halton Sequence (0) | 2022.06.10 |
| 균등난수(uniform random number) 만들어보자 #2 : LCG (0) | 2022.06.10 |
| 균등난수(uniform random number) 만들어보자 #1 (0) | 2022.06.08 |




댓글