미래주가의 분포를 활용하여 콜옵션 감마 구하기

 

 

이번 글은 미래주가의 분포를 활용하여 콜옵션 델타 구하기

미래주가의 분포를 활용하여 콜옵션 델타 구하기

에서 이어집니다. 위 글에서는 콜옵션의 델타(delta)를 미래주가의 분포를 이용하여 구하는 이론을 알아보았습니다.

그렇다면 감마(gamma)는 어떨까요?

 

먼저 지난 글에서 다루었던 내용을 간략하게 복습해 보겠습니다.

 

 

 

복습

글  GBM 모델로 생성된 주가의 누적분포함수, 확률밀도함수

GBM 모델로 생성된 주가의 누적분포함수, 확률밀도함수

에서 다룬 내용에서 

기초자산  $S_t$가 GBM 모델 
$$dS_t/S_t= (r-q) dt +\sigma dW_t$$
($r$는 무위험 이자율, $q$는 연속배당률,  $\sigma$는 변동성(volatility), 그리고 $W_t$는 위너프로세스)

을 따를 때, 만기 시점의 주가 $S_T$의 확률밀도함수와 누적분포함수는

 

$S_T$의	수식
누적분포함수 $F(x)$	$$F(x)=\Phi(d(x))$$ 여기서 $\Phi(\cdot)$는 표준정규분포의 누적분포함수이고 $$d(x) = \frac{\ln(x/S)-(r-q-\frac12\sigma^2)T}{\sigma\sqrt{T}}$$
확률밀도함수 $g(x)$	$$g(x)  = \frac{1}{x\sigma\sqrt{T}} \phi(d(x)),$$ 여기서 $\phi(\cdot)$는 표준정규분포의 확률밀도함수

와 같다고 했습니다.

 

이제 이 사실을 바탕으로 콜옵션의 감마를 구해보겠습니다.

 

 

콜옵션의 감마

 

만기 $T$이고 행사가 $K$인 유로피안 콜옵션의 가격 $c$는

$$c(S) = e^{-rT} \mathbb{E}(\max(S_T-K,0)) \tag{1}$$
입니다(현재시점 $t=0$에서의 옵션 가격으로 간주하여, $c$를 $S$에 대한 1 변수 함수로 표현하였습니다.)

위의 복습 파트에서, $S_T$의 확률밀도 함수를 $g(\cdot)$라 하였으므로 식(1)은

$$\begin{align}  c(S) & = e^{-rT} \int_0^\infty \max(x-K,0) g(x)dx\\       & =  \int_0^\infty e^{-rT}\max(x-K,0) g(x) \tag{2}dx \end{align}$$

변수 $x$는 $S_T$를 의미하고 $x$의 범위가 $(0,\infty)$이므로 적분 구간은 $(0,\infty)$가 됩니다.

 

감마는 파생상품의 가격을 기초자산으로 두 번 미분한 것이므로

$$\frac{\partial^2 C}{\partial S^2}$$

이죠. 이 값을 식(1)을 이용해 무작정 구해보도록 하죠.

$$\begin{align} \frac{\partial^2 c}{\partial S^2} & = \frac{\partial^2}{\partial S^2} \int_0^\infty e^{-rT}\max(x-K,0) g(x) dx\\ & =  \int_0^\infty \frac{\partial^2}{\partial S^2} \left( e^{-rT}\max(x-K,0) g(x) \right)dx\\ & =  \int_0^\infty e^{-rT}\max(x-K,0) \frac{\partial^2 g(x)}{\partial S^2} dx\\ & =  \int_0^\infty e^{-rT}\max(x-K,0) \frac{\partial^2 g(x)}{\partial S^2}  \frac{1}{g(x)} \cdot g(x) dx\\ & = \mathbb{E} \left(e^{-rT}\max(x-K,0) \frac{\partial^2 g(x)}{\partial S^2}  \frac{1}{g(x)}\right)\tag{3} \end{align}$$

이제 식(3)의 마지막 등식의 $\mathbb{E}(\cdot)$에 있는 수식

$$\frac{\partial^2 g(x)}{\partial S^2}  \frac{1}{g(x)}$$

을 보기 좋게 정리할 일만 남았습니다.

 

몇가지 소소한 계산을 미리 해놓자면, 

$$d(x) = \frac{\ln(x/S)-(r-q-\frac12\sigma^2)T}{\sigma\sqrt{T}}$$ 이므로

 

$$\frac{\partial d}{\partial S} =- \frac1{S\sigma\sqrt{T}} ~,~\frac{\partial^2 d}{\partial S^2} = \frac1{S^2\sigma\sqrt{T}} \tag{4}$$ 가 성립합니다.

 

또한 표준정규분포 확률밀도 함수 $\phi$는

 

$\phi'(x) =-x\phi(x)\tag{5}$ 이고
$$\phi''(x) =\frac{d}{dx}\phi'(x) = -\phi(x) -x\phi'(x) = -\phi(x) +x^2\phi(x)=(x^2-1)\phi(x)\tag{6}$$
를 만족합니다.

$$g(x) =\frac{\phi(d(x))}{x\sigma\sqrt{T}}$$ 이므로

$$\begin{align} \frac{\partial^2 g(x)}{\partial S^2}  \frac{1}{g(x)} & = \frac{1}{x\sigma\sqrt{T}}  \frac{\partial^2 \phi(d(x))}{\partial S^2}  \cdot \frac{x\sigma\sqrt{T}}{\phi(d(x))}\\ & = \frac{\partial}{\partial S} \left(\phi'(d(x)) \frac{\partial d(x) }{\partial S} \right) \cdot \frac{1}{\phi(d(x))} \\ & = \frac{1}{\phi(d(x))} \left( \phi''(d(x)) \Big(\frac{\partial d(x)}{\partial S}\Big)^2 + \phi'(d(x)) \frac{\partial^2 d(x) )}{\partial S^2} \right) \\ & =\frac{1}{\phi(d(x))} \left( \phi''(d(x)) \frac{1}{S^2\sigma^2 T} +\frac{1}{S^2\sigma\sqrt{T}}\phi'(d(x)) \right)~~ \because {\rm {by~ (4)}} \\ & = \frac{1}{\phi(d(x))} \left(  \frac{(d^2(x)-1)\phi(d(x))}{S^2\sigma^2 T} - \frac{d(x)\phi(d(x))}{S^2\sigma\sqrt{T}} \right)~~ \because {\rm {by~ (5),(6)}}\\  & = \frac{d(x)^2-d(x)\sigma\sqrt{T} -1}{S^2\sigma^2 T}\tag{7} \end{align}$$

입니다.  따라서 식(3)과 식(7)에 의해

 

$$\frac{\partial^2 c}{\partial S^2} = \mathbb{E} \left(e^{-rT}\max(x-K,0) \frac{d(x)^2+d(x)\sigma\sqrt{T} -1}{S^2\sigma^2 T} \right) \tag{8}$$

를 만족합니다. 이러한 방법을 likelihood 방법(우도비 방법)이라고 부릅니다.

 

 

식(8)은 다음과 같이 이용하면 됩니다.

 

○ 식(8)의 $x$는 만기종가를 뜻합니다. 즉, 어떤 표준정규분포를 따르는 난수 $z$에 대해

$$x= S \exp\left((r-q-\frac12\sigma^2)T +\sigma\sqrt{T}z\right)$$

로 생성할 수 있습니다.

 

○ $d(x)$ 를 계산해보면,

$$d(x) = \frac{\ln(x/S)-(r-q-\frac12\sigma^2)T}{\sigma\sqrt{T}} =z$$

 

이죠. 따라서, 

 

 $d(x)$는 표준정규분포 난수, $x$는 이 난수를 통해 만들어지는 GBM 만기 종가

 

라고 이해하면 될 것 같습니다. 이제 코딩을 통해 이 내용을 확인해보도록 하겠습니다.

 

 

 

 

Python Code

 

예전 글에서 구현해 놓았던 Closed form formula 관련 코드를 그대로 가져다 쓰겠습니다(관련 코드는 이런 글 등에서 찾아볼 수 있습니다.) 또는 바로 전 글 (미래주가의 분포를 활용하여 콜옵션 델타 구하기)의 코드 부분을 보셔도 됩니다.

 

또한 아래 코드는 바로 전 글의 코드와 너무나 흡사합니다. 밑의 코드의 estimator 변수만 식(7)의 공식으로 바꿔 주면 됩니다.

 

 

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import pandas as pd

# 아래는 call option delta의 수학 공식
def CallOptionBS(S, K, T, r, q, sigma):
    Ncdf = norm.cdf
    npdf = norm.pdf

    if T == 0:
        val = np.maximum(S - K, 0)
        delta = 1 if S >= K else 0
        gamma = 0
        speed = 0
        theta = 0
        vega = 0
        volga = 0
        ultima = 0

    else:
        d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
        d2 = d1 - sigma * np.sqrt(T)
        val = S * np.exp(-q * T) * Ncdf(d1) - K * np.exp(-r * T) * Ncdf(d2)
        delta = np.exp(-q * T) * Ncdf(d1)
        gamma = np.exp(-q * T) * npdf(d1) / (S * sigma * np.sqrt(T))
        speed = -np.exp(-q * T) * npdf(d1) / (S ** 2 * sigma * np.sqrt(T)) * (1 + d1 / (sigma * np.sqrt(T)))
        theta = -np.exp(-q * T) * S * npdf(d1) * sigma / (2 * np.sqrt(T)) - r * K * np.exp(-r * T) * Ncdf(
            d2) + q * S * np.exp(-q * T) * Ncdf(d1)
        # theta2 = -(r - q) * S * delta - 0.5 * sigma ** 2 * S ** 2 * gamma + r * val
        # theta +(r-q)S *delta + 0.5*sigma^2*S^2 *gamma -rf =0
        vega = S * np.exp(-q * T) * npdf(d1) * np.sqrt(T)  # vega
        volga = vega * d1 * d2 / sigma  # volga
        ultima = -vega / sigma ** 2 * (d1 * d2 * (1 - d1 * d2) + d1 ** 2 + d2 ** 2)  # ultima

    # return index
    # 0. value
    # 1. delta
    # 2. gamma
    # 3. speed
    # 4. theta
    # 5. vega
    # 6. volga
    # 7. ultima
    return val, delta, gamma, speed, theta, vega, volga, ultima

def call_option_gamma_likelihood(spot, strike, maturity, rfr, div, vol):
    np.random.seed(0)
    n_iter = 100000

    drift = rfr - div - 0.5 * vol ** 2
    diffusion = vol * np.sqrt(maturity)
    rand_vec = np.random.normal(size=n_iter)
    smat_vec = spot * np.exp(drift + diffusion * rand_vec)
    
    # 식(7)을 이용하여 estimator를 구성한다.
    estimator = np.exp(-rfr * maturity)* \
                np.maximum(smat_vec - strike, 0) * \
                (rand_vec**2 -rand_vec*vol*np.sqrt(maturity)-1)   / (spot**2 * vol**2 * maturity)
    call_gamma = estimator.mean()
    return call_gamma


def theoretical_vs_likelihood_call_gamma():
    strike = 100
    rfr = 0.02
    div = 0.01
    maturity = 1
    vol = 0.2
    s_vec = np.arange(10, 150, 1)

    theoretical_gamma = [CallOptionBS(s, strike, maturity, rfr, div, vol)[2] for s in s_vec]
    likelihood_gamma = [call_option_gamma_likelihood(s, strike, maturity, rfr, div, vol) for s in s_vec]

    max_diff = abs(np.array(theoretical_gamma) - np.array(likelihood_gamma)).max()

    print('maximum error is {:.6f}'.format(max_diff))  # 너무 차이가 작아 소수6째자리까지 표시
    plt.plot(s_vec, theoretical_gamma, label='theoretical gamma')
    plt.plot(s_vec, likelihood_gamma, label='likelihood gamma')
    plt.legend()
    plt.show()

if __name__ == '__main__':
    theoretical_vs_likelihood_call_gamma()

 

 

실행시키면 다음과 같습니다.

 

maximum error is 0.000380

너무 오차가 작아 code에 오차 수준을 소수 여섯째 자리까지 표기하는 걸로 바꿨을 지경입니다.

 

현재주가에 따른 이론적 감마와 위 이론의 감마를 그래프로 비교해 볼까요?

 

엄청난 정확성을 자랑함

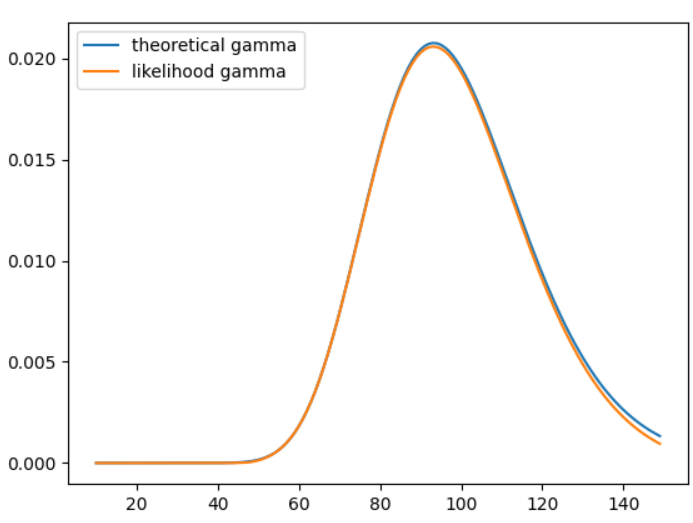
거의 완전히 일치하는 모양새를 볼 수 있습니다. 

감마를 시뮬레이션법으로 구했는데도 불구하고 엄청 정확하네요.

 

 

 

유한차분법으로 구한 감마보다 낫다!

 

전의 글 몬테카를로 시뮬레이션과 그릭의 안정성 #2 : 시드 고정

몬테카를로 시뮬레이션과 그릭의 안정성 #2 : 시드 고정

 

에서는 MC방법과 유한차분방법을 통해 그릭을 구하는 방법을 설명했었습니다. 시드를 고정시키고 세 값

$$c(t,S+\Delta S), c(t,S), c(t,S-\Delta S)$$

을 구한 뒤

 

$$\frac{c(t,S+\Delta S) - 2c(t,S) +c(t,S-\Delta S)}{\Delta S^2}$$

로 감마를 구할 수 있다 했습니다. 이  결과는 아래와 같이 나왔었고, 밑에 줄 왼쪽 그림이 감마를 표시한 그래프입니다.

 

 

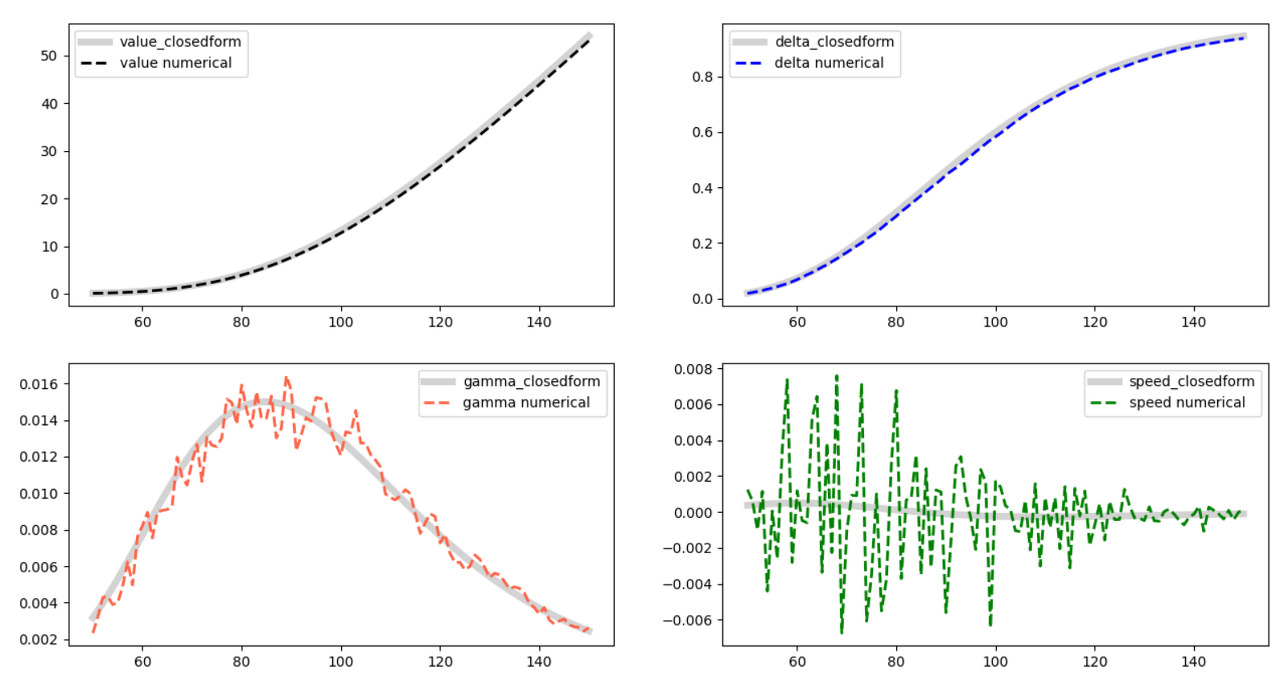
아무래도 세 개의 값을 각각 구해 차분법으로 구하니, 정확성도 떨어지고, 세 개의 값을 구하는데서 많은 시간이 소요됩니다.

 

하지만 식(7)의 결과 그래프를 보십시오. 엄청 아름답지 않나요?  값도 안정적이면서 계산시간도 짧은 아주 좋은 방법임을 알 수 있습니다. 

 

 

 

다음 글에서는 베가(Vega, 변동성에 대한 민감도)도  유사한 방법으로 어떻게 구할 수 있는지 알아보겠습니다.