이번 글은
2023.07.07 - [금융공학] - 몬테카를로 시뮬레이션과 그릭의 안정성 #1
몬테카를로 시뮬레이션과 그릭의 안정성 #1
이번 글은 2023.06.23 - [금융공학] - 그릭을 수치 해석적인 방법으로 해결하기 그릭을 수치 해석적인 방법으로 해결하기 이번 글은 2023.04.27 - [금융공학] - 델타, 감마, 스피드! 콜옵션의 가격 변화를
sine-qua-none.tistory.com
에서 이어집니다. 저번 글에서는 MonteCarlo Simulation이라는 방법을 사용하여 수치해석적으로 파생상품의 민감도를 구하는 과정을 다뤘습니다.
그런데 문제가 있었죠. 저번 글에서 봤던 그래프를 다시 한번 볼까요?
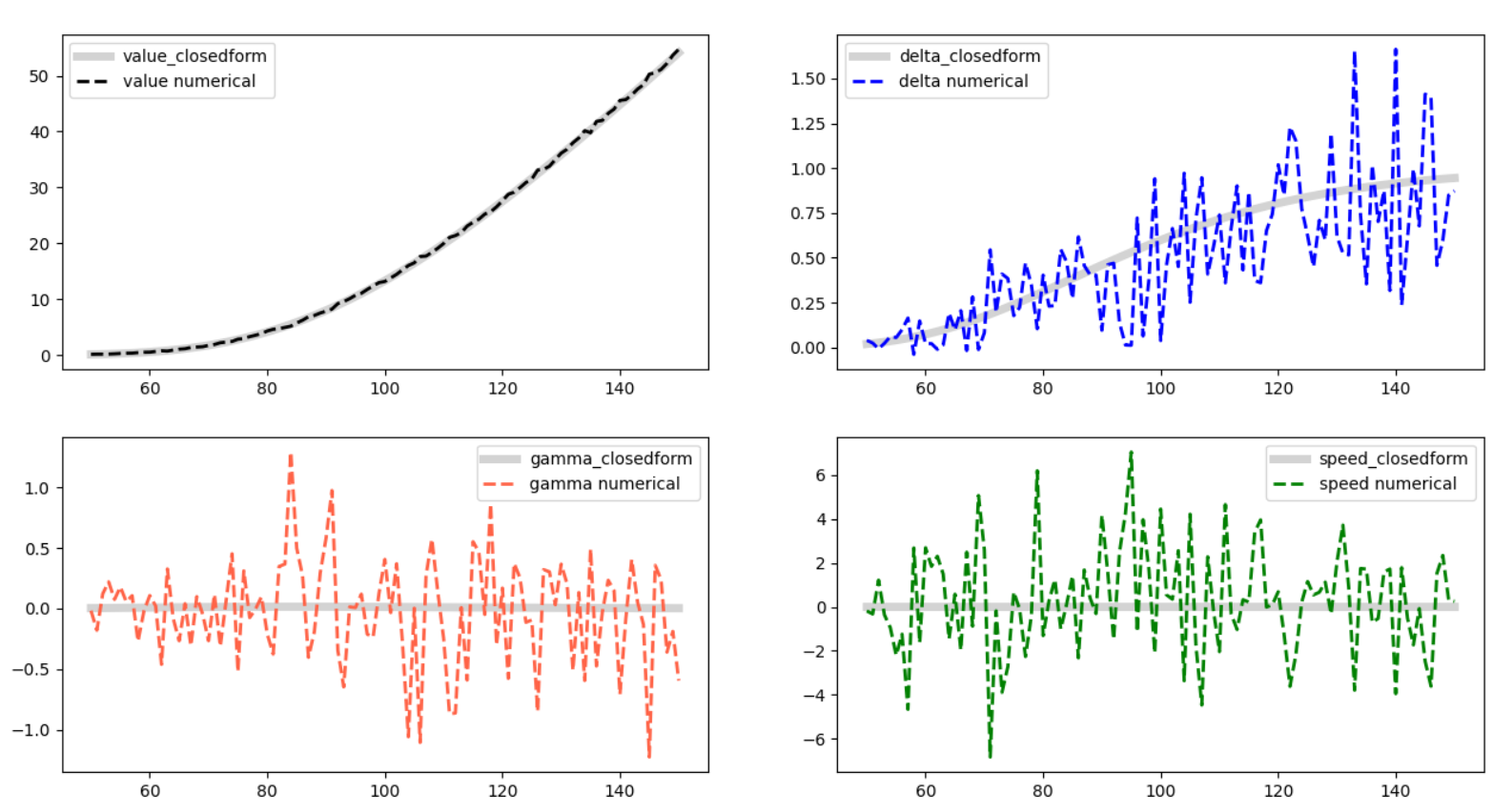
회색 실선이 콜옵션 closed form으로 추출한 가격 및 민감도(델타, 감마, 스피드), 각 색깔 점선이 MonteCarlo Simulation으로 유한차분법으로 구한 민감도였죠. 회색 실선이 0의 값으로 보일 정도로 색깔 점선들의 변동이 심합니다. 값이 불안정하죠.
왜 이러는 걸까요? 개선을 하지 않으면 쓰지 못할 값입니다.
문제는 주가 생성시 쓰는 난수!
MC(MonteCarlo Simulation)을 간략히 복습하자면 아래와 같습니다(콜옵션의 경우)
Step1. 난수를 아주 많이 생성한다.
Step2. 각 난수들을 사용하여 만기 종가 $S_T$를 뽑고 $\max(S_T-K,0)$ 의 콜옵션 페이오프를 각각 산출한다.
Step3. 위에서 구한 페이오프의 평균(기댓값)을 구한다.
Step4. Step3의 평균에 할인율을 곱하여 콜옵션 가격 산출!
시점 $t$, 기초자산 $S$에서의 콜옵션 가치를 $c(t, S)$라 한다면, 민감도, 예를 들어 델타는 다음과 같이 구합니다.
$$\Delta_c(t,S) = \frac{c(t,S+\frac12 dS)-c(t,S-\frac12 dS)}{dS}$$
따라서 좌변의 델타를 구하려면,
$$ c(t,S+\frac12 dS)\tag{1}$$ 와 $$c(t,S-\frac12dS)\tag{2}$$ 의 값을 각각 MC로 구해야 하죠.
그런데 그냥 아무생각없이 MC을 쓰면 Step1에서 난수를 뽑을 때, 식(1)을 위한 난수와 식(2)을 위한 난수가 아무렇게나 뽑힙니다.
이러면
가격 산출의 일관성이 깨져, 기초자산을 위, 아래로 올리고 내리는 효과가 없어지고, 잡음이 끼게 되는 현상
이 발생하죠. 간단한 코딩으로 알아보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import pandas as pd
def callvalue_by_MC_ver2(svalue, strike, maturity, rfr, div, vol, nIter):
drift = (rfr - div - 0.5 * vol ** 2) * maturity
volsqrtmat = vol * np.sqrt(maturity)
rvec = np.random.normal(size=nIter)
s_maturity = svalue * np.exp(drift + volsqrtmat * rvec)
payoff = np.array([np.maximum(0, s_mat - strike) for s_mat in s_maturity])
dfactor = np.exp(-rfr * maturity)
opt_value = payoff.mean() * dfactor
return opt_value, s_maturity # MC 방법과 똑같으나, 만기 종가 표본을 같이 리턴한다.
def callvalueGreeks_MC_ver2(svalue, strike, maturity, rfr, div, vol, nIter):
ds = svalue * 0.01
val, svec = callvalue_by_MC_ver2(svalue, strike, maturity, rfr, div, vol, nIter)
val_up, svec_up = callvalue_by_MC_ver2(svalue + ds / 2, strike, maturity, rfr, div, vol, nIter)
val_up2, svec_up2 = callvalue_by_MC_ver2(svalue + ds, strike, maturity, rfr, div, vol, nIter)
val_down, svec_down = callvalue_by_MC_ver2(svalue - ds / 2, strike, maturity, rfr, div, vol, nIter)
val_down2, svec_down2 = callvalue_by_MC_ver2(svalue - ds, strike, maturity, rfr, div, vol, nIter)
delta = (val_up - val_down) / (ds)
# S를 위, 아래 각각 dS/2만큼 bumping up/down 시킨 상황에서 난수 발생시켜 만든 종가들을
각각 return한다.
return val, delta, svec, svec_up, svec_down
def analysis_call_option_greeks_MC():
strike = 100
maturity = 1/12
rfr = 0.03
div = 0
vol = 0.3
nIter = 100
s=100
res_analytic = CallOptionBS(s, strike, maturity, rfr, div, vol) #closed form
val, delta, svec, svec_up, svec_down = callvalueGreeks_MC_ver2(s, strike, maturity, rfr, div, vol, nIter)
print(res_analytic[0]) #value
print(val)
plt.plot(np.sort(svec_up)) # delta 구할 떄 s+ds/2 에서 발생시킨 만기 종가들을 오름차순으로 정렬
plt.plot(np.sort(svec_down)) # delta 구할 떼 s-ds/2에서 발생시킨 만기 종가들을 오름차순으로 정렬
plt.show()
즉, 위 코드는
식(1)을 산출할 때 필요한 만기종가 샘플을 오름차순으로 정렬한 것과
식(2)을 산출할 때 필요한 만기종가 샘플을 오름차순으로 정렬한 것을
같이 그려보는 것입니다. 우리 생각에는 이 두 plot이 평행하게 나와야 정상일 것 같은데요, 결과를 보면,

이렇게 됩니다(편의상 한 눈에 파악하기 위해 MC 시뮬레이션 횟수를 100으로 작게 잡았습니다.)
어떤가요? 두 만기종가 샘플이 평행하지 않고 교차하게 되고 이상합니다. 이 현상을 고치는 방법은 간단합니다.
바로 아래처럼 하면 되죠.
난수의 시드를 고정하자.
난수의 시드(seed)를 고정하게 되면, 프로그램이 실행될 때마다 같은 난수를 발생하게 되어, 결과가 아름다워집니다.
위의
def callvalue_by_MC_ver2(svalue, strike, maturity, rfr, div, vol, nIter):함수의 첫 줄에
np.random.seed(0)를 추가해 보죠. 시드를 고정시키자는 의미입니다. 시드값인 0 자리에 아무 값이나 넣어도 상관없습니다. 어쨌든 시드 0에서 출발하여 어떤 내재적으로 정해진 알고리즘으로 같은 난수들이 발생되는 효과이죠. 이제 이 한 줄 넣고 결과를 뽑아보면,

아주 그래프가 예쁘게 평행하게 나온다는 것을 알 수 있습니다. 보다 자세히 들여다보기 위해 $y$축을 좀 제한시키고, 색깔을 예쁘게 입혀서 살펴보죠. 위 코드의 plotting 부분을
plt.plot(np.sort(svec_up), label='svec_up', c='gray')
plt.plot(np.sort(svec), label='svec', c='black')
plt.plot(np.sort(svec_down), label='svec_down', c='gray')
plt.ylim(90, 110)
plt.legend()
plt.show()이렇게 바꿔서 그려보면,

위와 같이 됩니다. 검은 선이 기초자산 $S$에서 시작한 만기 종가들을 나래비 세운 그림이고, 위아래 회색선은 $S+dS/2$와 $S-dS/2$에서 출발한 만기종가들 선입니다.
이게 맞아 보입니다. 따라서 MC 시뮬레이션을 할 때는 시드를 고정시켜 주어야 합니다.
시드를 고정한다면?
전 글 (몬테카를로 시뮬레이션과 그릭의 안정성 #1)에 등장하는 MC 함수
def callvalue_by_MC(svalue, strike, maturity, rfr, div, vol, nIter):의 첫 줄에
np.random.seed(0)만 넣어서 결과를 보죠.

Maximum difference between closed form delta and MC delta : 0.0193946612
Maximum difference between closed form gamma and MC gamma : 0.0023615467
Maximum difference between closed form speed and MC speed : 0.0071741471
어떤지요? 델타는 아주 정확하지 않습니까? 시드만 고정시켜 준 효과입니다. 다만, 감마, 스피드는 아무래도 불안정하군요.
보다 많은 샘플을 추출하여 MC를 시뮬레이셔하면 이 값도 정확 해질 텐데, 계산 시간이 다소 많이 소요되는 단점은 있습니다. (아래 더보기 를 클릭하여 저번 글의 결과와 비교해 보세요.)

Maximum difference between closed form delta and MC delta : 0.7694295983
Maximum difference between closed form gamma and MC gamma : 1.2779184401
Maximum difference between closed form speed and MC speed : 7.0555037445
결론
MC 시뮬레이션을 이용하여 파생상품의 가격을 구할 때는 가격 및 민감도 안정성을 위해
시드를 고정하는 것
이 효율적입니다.
민감도까지 언급할 필요 없이, 시드를 고정시키지 않은 상태에서 콜옵션 가격을 구하면, 구할 때마다 값이 다르게 산출됩니다. 이것 또한 말이 안 되죠.
여러모로 시드를 고정해야 합니다.
시드는 어떤 값으로 고정하냐의 문제가 있을 수는 있는데, 다양한 시드를 바꿔가며 값을 산출해 보고, 이것이 closed form과 가장 가까워지는 시드를 찾아도 되고, 그때 그때 상황에 맞게 찾으시면 되겠습니다.
'금융공학' 카테고리의 다른 글
| GBM 모델로 생성된 주가의 누적분포함수, 확률밀도함수 (0) | 2023.08.08 |
|---|---|
| MC로 콜옵션 델타 구하기: likelihood 방법 (0) | 2023.07.14 |
| 몬테카를로 시뮬레이션과 그릭의 안정성 #1 (0) | 2023.07.07 |
| 그릭을 수치 해석적인 방법으로 해결하기 (0) | 2023.06.23 |
| 풋옵션의 민감도들은? feat. 풋콜패리티 (0) | 2023.06.19 |




댓글