워스트 퍼포머(worst performer)의 분포 #1

이 글은

2022.10.24 - [금융공학] - 자산의 퍼포먼스(performance)와 워스트포퍼머(worst performer)

자산의 퍼포먼스(performance)와 워스트포퍼머(worst performer)

에서 이어집니다. 지난 글에서는 여러 개의 주식이 주어져 있을 때, 

○ 각 주식의 퍼포먼스(performance)를 정의하고

○ 이 중, 가장 성과가 떨어지는 워스트 퍼포머(worst performer)라는 시계열을 정의해 보았습니다.

 

워스트 포퍼머는 금융상품의 기초자산으로 널리 쓰이고, 특히 ELS 등 파생상품의 설계에 긴요하게 쓰이는 개념입니다. 따라서 워스트 포퍼머를 잘 이해하는 것이 필요합니다.

 

꼴찌인 나를 좀 이해해줘~

 

우선, 주식의 갯수는 2개, 모든 주식의 움직임을 GBM으로 가정하겠습니다. 즉, 주식 $X_1, X_2$ 에 대해

$$dX_i(t)/X_i(t) = (r-q_i) dt + \sigma_i dW_i(t)~~,~~i=1,2  \tag{1}$$

라 가정해보죠.  그리고 두 자산의 로그수익률의 상관계수를 $\rho$라 합시다. 즉,

$$dW_1 dW_2 =\rho dt$$

인 상황입니다([금융공학] - 상관관계를 보이는 두 자산의 움직임 모델을 참고해 보면 됩니다.)

 

한 가지 중요한 점이 원래 주식 모델이 GBM이면, 그것의 퍼포먼스도 GBM이죠. 당연한 것이, 퍼포먼스라는 것은 원래 주가를 어떤 기준가로 나눈 것에 불과하기 때문입니다.  예를 들어 $X(t)$라는 주식이 GBM $dX(t)/X(t) =\mu dt+\sigma dW_t$를 따른다면, 기준점 $X(0)$로 나눈 새로운 프로세스

$$x(t) = \frac{X(t)}{X(0)}$$ 의 다이나믹은

$$dx(t)/x(t) = \frac{dX(t)}{X(0)} \Big / \frac{X(t)}{X(0)}= dX(t)/X(t) = \mu dt +\sigma dW_t$$

처럼 원래 주식과 동일한 GBM 이 됩니다.

 

따라서 우리는 식(1)의 $X_i$들을 주식이 아닌 퍼포먼스라 생각해도 무방합니다.

 

 

 

워스트 퍼포먼스의 분포를 구해보자

식(1)에서 정의한 두 퍼포먼스 $X_1, X_2$의 워스트 포퍼머의 분포를 구해볼까 합니다.

 

1 변수 표준 정규분포의 누적분포 함수(cdf)를 $\Phi(\cdot)$, 이변량 표준정규분포의 누적분포함수(cdf)를 $\Phi_2(\cdot ; \rho)$ 라 합시다. 이와 같이 쓰는 이유는 표준 정규분포를 가정하므로 평균은 모두 0, 분산은 1인 상황이라 누적분포함수의 모양은 두 변수의 상관계수에만 의존하게 되겠죠.

 

식(1)의 $X_1(t), X_2(t)$의 기준시점에서의 퍼포먼스를 각각 $x_1, x_2$라 하면,

$$X_i(t)= x_i \exp \left( (r-q-{\textstyle{\frac12}}\sigma_i^2 ) t + \sigma_i W_i(t) \right) ~~,~~ i=1,2$$

가 됩니다.

(시점 $t=0$에서 따지면 $x_i$들은 무조건 1인데요, 위에서는 특정 시점의 퍼포먼스 초기값과 잔존만기를 생각하여 $x_i$라는 값으로 살려둔 것입니다.)

 

많이 다루었다시피 $i=1,2$에 대해 , $W_i(t) = \sqrt{t} z_i~,~ z_i \sim \mathcal{N}(0,1)$ 이고, 상관계수를 도입하면

$$\mathbb{Corr}(z_1, z_2)=\rho$$

입니다.(서서히 이변량 표준 정규분포를 쓸 수 있는 모습이 되가죠?)

 

간단한 표기를 위해

$$\mu_i  :=r-q-\textstyle{\frac12}\sigma_i^2 ~,~i=1,2$$

라 정의합니다. 그러면 최종적으로

 

$$X_i(t)= x_i \exp \left( \mu_i t + \sigma_i \sqrt{t} z_i \right) ~~,~~ i=1,2\tag{2}$$

이고 $\mathbb{Corr}(z_1,z_2)=\rho$입니다.

 

 

드디어 워스트 퍼포머의 분포를 구할 준비가 끝났습니다.  워스트 퍼포머를 $wp(t):=\min(X_1(t), X_2(t))$ 라 합시다. 우리의 목적은 실수 $K$에 대해

$$\mathbb{P}(wp(t)\leq K)$$

의 값을 구하는 것입니다. 

 

$$\begin{align} \mathbb{P}(wp(t)\geq K) & = \mathbb{P}(\min(X_1(t),X_2(t))\geq K)\\ & = \mathbb{P} (X_1(t) \geq K \rm{~and~} X_2(t) \geq K) \\ & = \mathbb{P} (\ln(X_1(t))\geq \ln K \rm{~and~} \ln(X_2(t)) \geq \ln K)\tag{3} \end{align}$$

 

두 번째 등식은 $\min(x,y)\geq K \Leftrightarrow (x\geq K) \cap (y\geq K)$ 의 성질이 쓰였고, 세 번째 등식은 $x\geq K \Leftrightarrow \ln x \geq \ln K$의 성질이 쓰였습니다. 

 

식(3)을 이어나가기 위해, 식(2)을 대입하면

$$\begin{align} \mathbb{P} (\ln(X_1(t))\geq \ln K & \rm{~and~} \ln(X_2(t)) \geq \ln K)\\  &= \mathbb{P}\left( z_1 \geq \frac{\ln(K/x_1)-\mu_1 t}{\sigma_1\sqrt{t}} ,z_2 \geq \frac{\ln(K/x_2)-\mu_2 t}{\sigma_2\sqrt{t}} \right) \\ & = \mathbb{P}(z_1\geq \alpha_1 , z_2 \geq \alpha_2)\tag{4} \end{align}$$

입니다. 여기서 편의를 위해

$$\alpha_i = \frac{\ln(K/x_i)-\mu_i t}{\sigma_i\sqrt{t}}~,~i=1,2$$ 라 정의했습니다.

 

 

이제 식(4)만 구하면 됩니다. 식(4)에서 확률을 구하는 영역은 아래 그림(파란색 영역)입니다.

 

파란색 영역

 

이는 여집합을 생각하여 아래 그림처럼 구할 수 있죠(오렌지색 영역)

 

전체영역에서 오렌지색을 빼주면 됨

 

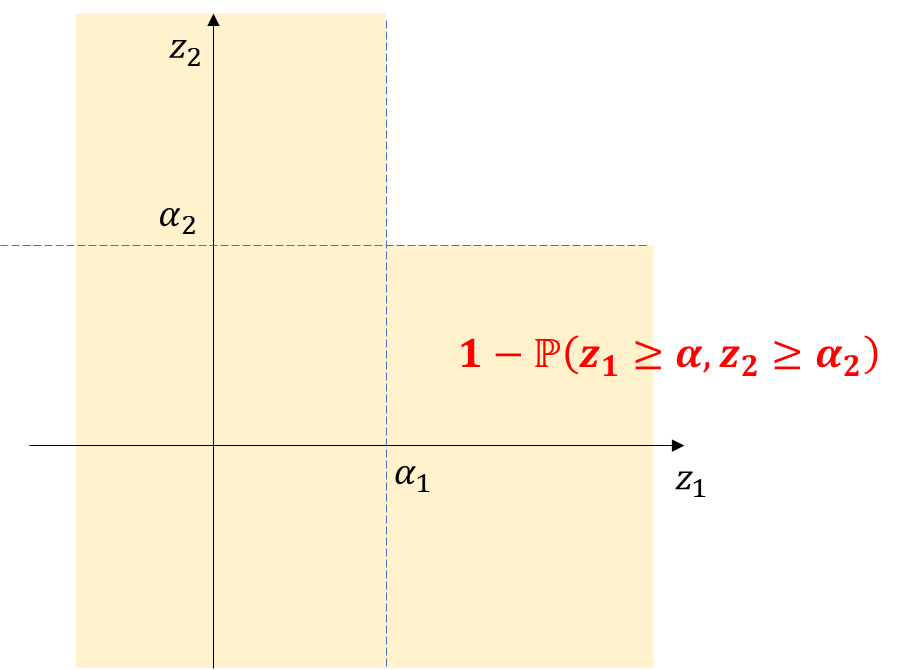
이 영역은 다시 아래 두 영역을 합쳐준 뒤(회색 영역 2개)

겹치는 부분이 있다!

 

겹치는 부분인 아래 그림의 녹색 영역을 빼주면 됩니다.

 

 

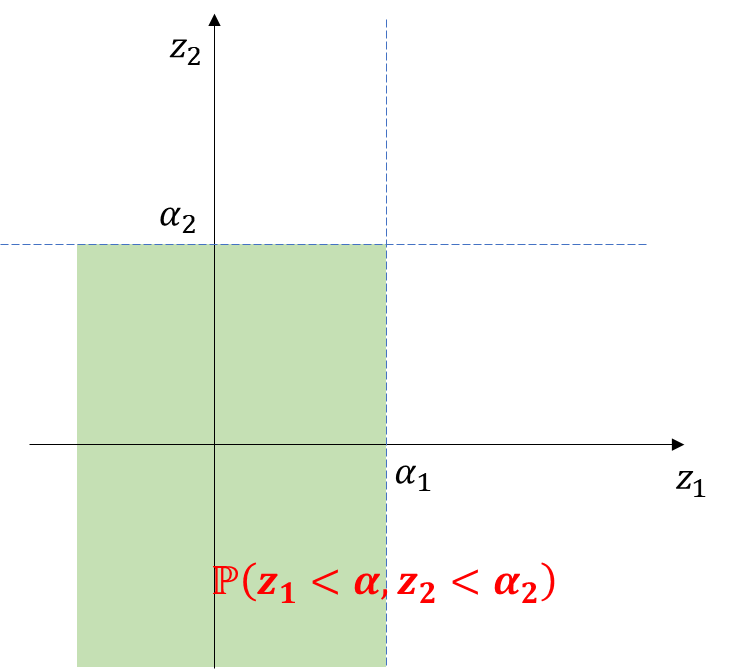
그림으로 이해한 바를 수식으로 써보면,

$$\mathbb{P}(z_1\geq \alpha_1 , z_2 \geq \alpha_2) =  1-\left[\mathbb{P}(z_1\leq \alpha_1) +\mathbb{P}(z_2\leq \alpha_2) -\mathbb{P}(z_1\leq \alpha_1 , z_2 \leq \alpha_2) \right]\tag{5}$$

입니다.

그런데 위 식 우변의 등장한 세 개의 항은 각각 무엇일까요? marginal distribution을 생각해보면 바로

 

$$\begin{align} \mathbb{P}(z_1\leq \alpha_1) & = \Phi(\alpha_1)\\ \mathbb{P}(z_2\leq \alpha_2) & = \Phi(\alpha_2)\\ \mathbb{P}(z_1\leq \alpha_1 , z_2 \leq \alpha_2) &= \Phi_2(\alpha_1, \alpha_2 ; \rho)\tag{6} \end{align}$$

이죠. 결론적으로 식(3)~(6)을 쭉 이어 보면

 

$$\mathbb{P}(wp(t)\geq K) = 1- \Phi(\alpha_1)-\Phi(\alpha_2) +\Phi_2(\alpha_1, \alpha_2 ; \rho)$$

 

를 얻습니다. 

 

$wp(t)$의 누적분포함수(cdf)를 $F_{wp}(K)$ 라 하면, $F_{wp}(K) =\mathbb{P}(wp(t)\leq K)$ 이므로 최종적으로 아래와 같이 정리할 수 있습니다.

 

기초자산 $X_1, X_2$ 의 워스트포퍼머는 다음과 같은 누적분포함수 $F_{wp}(K)$를 따른다.

$$F_{wp}(K) = \Phi(\alpha_1)+\Phi(\alpha_2) -\Phi_2(\alpha_1, \alpha_2 ; \rho)$$
여기서
$$\alpha_i = \frac{\ln(K/x_i)-\mu_i t}{\sigma_i\sqrt{t}}~,~i=1,2$$
이다.

 

다음 글에서 이 식이 맞는지를 이 식으로 직접 구한 결과와 몬테카를로 시뮬레이션 방법으로 구한 결과를 비교하여 서로 크로스 체킹 하여보겠습니다.