이 글은
2022.09.30 - [금융공학] - 상관관계가 있는 두 자산이 움직이는 모습은?
상관관계가 있는 두 자산이 움직이는 모습은?
이 글은 2022.09.30 - [금융공학] - 상관관계를 보이는 두 자산의 움직임 모델 상관관계를 보이는 두 자산의 움직임 모델 파생상품은 기초자산의 움직임에 연동하여 수익이 결정되는 금융상품이라
sine-qua-none.tistory.com
의 확장판입니다. 이번 글에서는 3개의 자산이 상관관계를 가질 때, 어떻게 움직이는지를 알아보려 합니다.
복습
세 자산을 $X_1, X_2, X_3$라 하고 GBM을 따른다고 합시다. 즉, $i=1,2,3$에 대해
$$ dX_i(t)/X_i(t) = (r-q_i)dt + \sigma_i dW_i(t)$$
입니다. $q_i$와 $\sigma_i$는 $i$번째 자산의 연속 배당률, 변동성입니다. $r$은 무위험 이자율입니다.
$X_i$와 $X_j$ 각각의 로그수익률의 상관계수를 $\rho_{ij}$라 하고 이를 원소로 하는 상관계수 행렬을 $\mathbf{R}$이라 하면, $\mathbf{R}$은 촐레스키 분해를 통해
$$\mathbf{R} = \mathbf{L}\mathbf{L}^t$$
로 나눠지고 서로 독립인 표준 정규분포 난수 $z_1, z_2, z_3$을 추출하여
$$
\frac{1}{\sqrt{\Delta t}}
\begin{pmatrix}
W_1(t)\\ W_2(t) \\ W_3(t)
\end{pmatrix}
=
\mathbf{L}
\begin{pmatrix}
z_1\\z_2\\ z_3
\end{pmatrix}
$$
와 같이 $W_1(t), W_2(t), W_3(t)$를 얻어내면, 자산 3개에 상관관계를 줄 수 있습니다. 이를 이용해 $i=1,2,3$에 대하여
$$
\begin{align}
X_1{t+\Delta t} &= X_1(t) \exp \left((r-q_1-\textstyle{\frac12}\sigma_1^2)\Delta t + \sigma_1 W_1(\Delta t) \right)\\
X_2{t+\Delta t} &= X_2(t) \exp \left((r-q_2-\textstyle{\frac12}\sigma_2^2)\Delta t + \sigma_2 W_2(\Delta t) \right) \\
X_3{t+\Delta t} &= X_3(t) \exp \left((r-q_3-\textstyle{\frac12}\sigma_3^2)\Delta t + \sigma_3 W_3(\Delta t) \right)\\
\end{align}
$$
처럼 재귀적으로 주가 패스를 생성할 수 있습니다.
Python Code : 상관관계가 있는 세 자산의 움직임
import numpy as np
import matplotlib.pyplot as plt
import pprint
import scipy
import scipy.linalg
from mpl_toolkits.mplot3d import Axes3D
def Generate_3Assets_GBM():
s = np.ones((1, 3)) * 100
q = np.zeros((1, 3))
v = np.array([[0.1, 0.2, 0.3]])
rfr = 0.02
mat = 1
rho12, rho13, rho23 = 0.7, -0.7, 0
CorrMat = np.array([[1, rho12, rho13],
[rho12, 1, rho23],
[rho13, rho23, 1]])
L_scipy = scipy.linalg.cholesky(CorrMat, lower=True)
pprint.pprint(L_scipy)
drift = (rfr - q - 0.5 * v * v) * mat
diffusion = v * np.sqrt(mat)
norm_rand = np.random.normal(size=(3, 1000))
corr_norm_rand = L_scipy @ norm_rand
res = s * np.exp(drift + diffusion * corr_norm_rand.T)
pprint.pprint(res)
s1_mat = res[:, 0]
s2_mat = res[:, 1]
s3_mat = res[:, 2]
fig = plt.figure(figsize=(20, 20))
gs = fig.add_gridspec(3, 2)
ax = fig.add_subplot(gs[:, 0], projection='3d')
ax.scatter(s1_mat, s2_mat, s3_mat, c='b', marker='o', s=15, cmap='Greens')
ax.set_xlabel('s1')
ax.set_ylabel('s2')
ax.set_zlabel('s3')
ax.view_init(30, 60)
ax2 = fig.add_subplot(gs[0, 1])
ax2.scatter(s1_mat, s2_mat, c='m')
ax2.set_title('s1 vs s2 (corr:{:.1f})'.format(CorrMat[0, 1]))
ax3 = fig.add_subplot(gs[1, 1])
ax3.scatter(s1_mat, s3_mat, c='c')
ax3.set_title('s1 vs s3 (corr:{:.1f})'.format(CorrMat[0, 2]))
ax4 = fig.add_subplot(gs[2, 1])
ax4.scatter(s2_mat, s3_mat, c='gray')
ax4.set_title('s2 vs s3 (corr:{:.1f})'.format(CorrMat[1, 2]))
plt.show()
if __name__ == '__main__':
Generate_3Assets_GBM()
code를 간략히 살펴보겠습니다.
import pprint #print를 예쁘게 해주는 라이브러리
import scipy # Cholesky 분해를 하기위한 scipy라이브러리
import scipy.linalg #scipy내에 linear algebra 모듈안에 Cholesky분해가 있음
def Generate_3Assets_GBM():
s = np.ones((1, 3)) * 100 # 3개 자산의 현재가
q = np.zeros((1, 3)) # 연속배당률
v = np.array([[0.1, 0.2, 0.3]]) # 변동성을 각각 10%, 20%, 30$
rfr = 0.02 # 무위험 이자율
mat = 1 # 만기
rho12, rho13, rho23 = 0.7, -0.7, 0 #기초자산간 correlation, rho12는 Asset1, Asset2의 corr
CorrMat = np.array([[1, rho12, rho13],
[rho12, 1, rho23],
[rho13, rho23, 1]]) # correlation matrix 생성
L_scipy = scipy.linalg.cholesky(CorrMat, lower=True) #correlation matrix를 Cholesky분해
pprint.pprint(L_scipy) # 하삼각행렬 출력○ scipy.linalg.cholesky의 용법은 촐레스키 분해 글을 참조해보면 됩니다.
○ CorrMat 변수가 positive definite가 아닐 경우, 오류가 날 수 있습니다. 그만큼 상관계수 행렬을 만들 때 주의해야 합니다.
drift = (rfr - q - 0.5 * v * v) * mat # 3 asset의 drift term 산출 (1*3 배열)
diffusion = v * np.sqrt(mat) # 3 asset의 diffusion term 산출 (1*3 배열)
norm_rand = np.random.normal(size=(3, 1000))
# 1000개의 sample을 위해 서로 독립인 표준정규분포 3*1000 배열 추출
corr_norm_rand = L_scipy @ norm_rand
# Cholesky 분해의 결과를 곱하여 상관관계를 줌
# 각각의 열은 세 개의 행으로 이루어져있고, 이 세개의 값이 correlated 됨
res = s * np.exp(drift + diffusion * corr_norm_rand.T)
# 1000 * 3 배열의 만기 종가를 얻음. 1000개의 각 행은 세 개의 원소로 이루어져있고
# 이 각각이 Asset1~3의 만기 종가임○ 배열의 size를 맞춰 계산해 보면 이해하는데 어려움이 없을 것 같습니다.
s1_mat = res[:, 0] # Asset1의 1000개 sample 만기 종가
s2_mat = res[:, 1] # Asset2의 1000개 sample 만기 종가
s3_mat = res[:, 2] # Asset3의 1000개 sample 만기 종가
fig = plt.figure(figsize=(20, 20))
gs = fig.add_gridspec(3, 2)○ add_gridspec 은 차트를 그릴 fig 판에 grid를 specify 하는 함수입니다. 3 by 2 (행으로 3개, 열로 2개)로 grid를 줍니다.
ax = fig.add_subplot(gs[:, 0], projection='3d')
# grid판의 첫째 열을 통째로 선택한 후, 3dimension 그래프를 그릴 예정
ax.scatter(s1_mat, s2_mat, s3_mat, c='b', marker='o', s=15, cmap='Greens')
ax.set_xlabel('s1')
ax.set_ylabel('s2')
ax.set_zlabel('s3')
ax.view_init(30, 60) #3차원 그래프를 z축으로 회전, xy평면으로 회전하는 양을 뜻함○ view_init(elev=None, azim=None, roll=None, vertical_axis='z') 는 vertical axis인 z 축으로 elev 만큼 회전시켜 보고, xy평면으로 방위각(azim, azimuth) 만큼 돌려서 보겠다는 함수입니다. 자세한 용법은 여기를 참고해 보시기 바랍니다.
ax2 = fig.add_subplot(gs[0, 1]) # grid의 첫번째 행, 2번째 열 위치에 ax2 축을 설정하고
ax2.scatter(s1_mat, s2_mat, c='m') # asset1, 2의 위치관계를 분산표로 그려봄
ax2.set_title('s1 vs s2 (corr:{:.1f})'.format(CorrMat[0, 1])) #제목 설정
결과
결과는 다음과 같습니다.
array([[ 1. , 0. , 0. ],
[ 0.7 , 0.71414284, 0. ],
[-0.7 , 0.68613724, 0.19802951]])
array([[103.39437798, 111.01573218, 113.48193985],
[100.86357257, 104.77423869, 105.70816961],
[114.77778009, 113.54511992, 73.54616761],
...,
[119.84121904, 116.0727373 , 56.1370187 ],
[ 94.63060179, 108.29100239, 144.29630674],
[124.68773424, 136.37682264, 58.05831343]])○ 위의 array가 촐레스키 분해의 결과입니다.
○ 아래 array는 3개 자산의 만기 종가 sample 1,000개를 의미합니다.
차트 결과는 아래와 같습니다. 3차원 그래프로 세 자산의 위치 관계를 한눈에 볼 수도 있고, 두 개씩 선택하여 경향성을 볼 수도 있습니다.
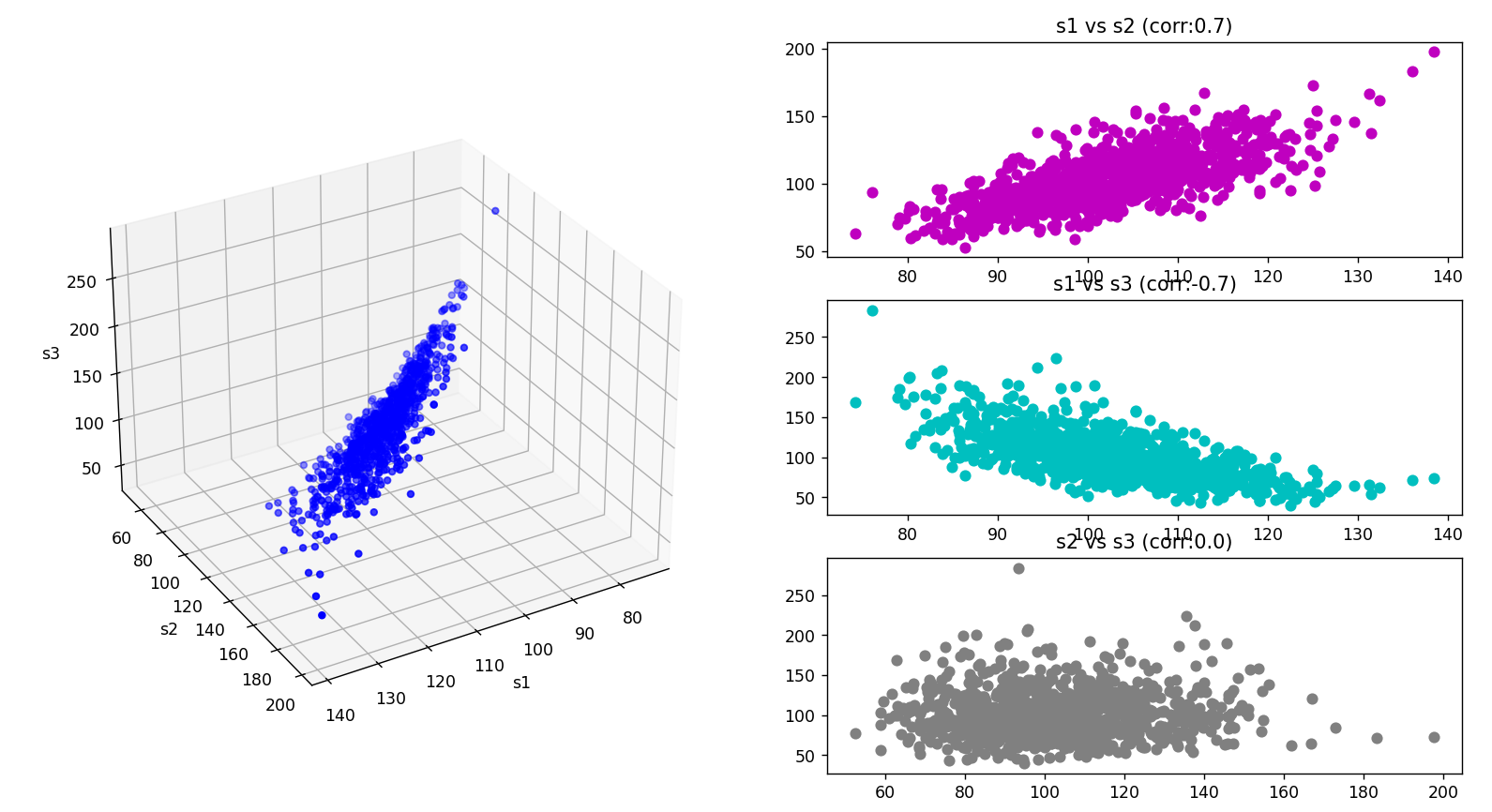
다음 글에서는 실제 지수나 주가를 가지고 어떻게 상관계수를 구하는지, 차트로는 어떻게 표현할 수 있는지 알아보겠습니다.
'금융공학' 카테고리의 다른 글
| 자산의 퍼포먼스(performance)와 워스트포퍼머(worst performer) (0) | 2022.10.24 |
|---|---|
| 상관관계가 있는 실제 주가의 움직임 (0) | 2022.10.21 |
| 상관관계가 있는 여러 자산이 움직이는 모습 (0) | 2022.10.13 |
| 상관관계가 있는 두 자산이 움직이는 모습은? (0) | 2022.09.30 |
| 상관관계를 보이는 두 자산의 움직임 모델 (0) | 2022.09.30 |



댓글