이번 글은
2022.06.15 - [수학의 재미/확률분포] - 정균분포 난수를 만들어 주세요 #4 : Box-Muller 방법
정균분포 난수를 만들어 주세요 #4 : Box-Muller 방법
이번 글은 2022.06.14 - [수학의 재미/확률분포] - 정균분포 난수를 만들어 주세요 #3 : Normal CDF 이용 정균분포 난수를 만들어 주세요 #3 : Normal CDF 이용 이번 글은 2022.06.13 - [수학의 재미/확률분포] -..
sine-qua-none.tistory.com
에서 이어집니다. Box-Muller 방법을 복습해보면,
Box Muller Method
균등분포 난수 $u,v \sim \mathcal{U}[0,1]$를 뽑아
$$ x= \sqrt{-2\ln u} \cos(2\pi v) ~,~ y=\sqrt{-2\ln u} \sin(2\pi v) $$
라 하면 $x,y$는 서로 독립이고, 표준정규분포 $\mathcal{N}(0,1)$을 따른다.
입니다. 공식을 보면 $\ln,~ \cos,~\sin$ 등 계산시간이 많이 걸리는 함수들이 난무하죠? 그래서 이러한 함수들을 최대한 안 쓰고자 하는 연구가 많이 이뤄졌습니다. 그중에 제법 잘 알려진 Marsaglia-Bray Method 가 있습니다.
Box-Muller method 의 $2\pi v$는 사실 $[0,2\pi]$ 구간의 각(angle) 역할을 했습니다. 그러면 어떤 실수 $x,y\in\mathbb{R}$에 대해,
$$ \cos(2\pi v) = \frac{x}{\sqrt{x^2+y^2}}~,~ \sin(2\pi v) = \frac{y}{x^2 +y^2} $$
입니다. 실수 $(x,y)$를
$$ x^2+y^2 \leq 1$$
을 만족하도록 잡습니다. 즉 $(x,y)$는 아래 그림처럼 단위 원 내부의 점입니다.

왜 단위원을 잡을까요? 지금 Box-Muller의 $\cos(2\pi v)$ 과 $\sin(2 \pi v)$ 를 없애면서 $\frac1{\sqrt{x^2+y^2}} (x,y)$ 로 바꿨죠? $v$라는 한 변수를 없애고 $x,y$ 두 변수가 됐습니다. 어째 효율적이지 않죠. Box-Muller의 또 다른 변수인 $u$를 그대로 가져다 사용하면 $x,y,u$ 세 변수가 되어 버립니다. 효율성이 제로죠. 따라서 $u$를 $x,y$로 만들어서, 구체적으로 얘기하면
$$ u= x^2+y^2 $$
으로 세팅해서 쓰겠다는 것입니다. 만일 $(x,y)$가 단위원 내부에 있으면 $u$는 0과 1 사이의 숫자가 되겠죠. 이제 이걸 정리하면 다음의 Marsaglia-Bray method을 얻게 됩니다.
Marsaglia-Bray method
$(x,y)$ 가 $x^2 +y^2 \leq 1$을 만족할 때,
$$z_1 = x \sqrt{\frac{-2\ln(s)}{s}}~,~ z_2 = y \sqrt{\frac{-2\ln(s)}{s}}$$
은 일차독립이고 표준정규분포를 따른다. 여기서 $s=x^2 +y^2$이다.
자 그럼 $x,y$를 어떻게 뽑을 수 있을까요? 점 $(x,y)$가 단위 원안에 있게끔요. 우선 단위원을 품는 정사각형을 하나 잡습니다.

그러면 파란 정사각형 안의 점은 $-1\leq x \leq 1~,~ -1\leq y \leq 1$을 만족합니다. 어떻게 뽑아내면 될까요? 바로
uniform random number 두 개를 골라서 $u,v$ 라 하면
$$ x=2u-1~, y= 2v-1$$가 정사각형 안의 점이겠죠. 그런 다음
$$ x^2 +y^2$$
값을 계산해 보는 겁니다. 이 값이 $1$보다 크면 이 점은 버리고, $1$보다 작으면 선택합니다.
정리하면 다음과 같습니다.
- uniform random number $u,v$를 고른다.
- $ x=2u-1$, $y=2v-1$ 을 한다.
- $x^2 +y^2 \leq 1$ 를 만족하는지 판단한다.
- Marsaglia-Bray method 를 사용하여 표준정규분포를 따르는 난수를 만든다.
python code를 보시겠습니다.
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def marsaglia_sample(n=1):
def marsaglia():
while True:
w1 = (np.random.rand() * 2) - 1
w2 = (np.random.rand() * 2) - 1
s = w1 * w1 + w2 * w2
if s < 1:
t = math.sqrt((-2) * math.log(s) / s)
z1, z2= w1 * t, w2*t
return z1, z2
z1 = np.empty(n)
z2 = np.empty(n)
for i in range(n):
z1[i], z2[i] = marsaglia()
return z1, z2
if __name__ == '__main__':
res= marsaglia_sample(n=3)
print(res)
print(type(res[0]))Box-Muller 함수와 마찬가지로 Size가 있는 정규분포 난수 배열을 얻는 함수입니다.
결과는 다음과 같습니다.
(array([ 0.38530066, 0.9451111 , -0.77982847]), array([ 1.96944666, -1.77520716, -0.47593814]))
<class 'numpy.ndarray'>
Process finished with exit code 0
그럼 Marsaglia 방법이 정말 정규분포를 추출하는지 python code로 확인해볼까요?
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def marsaglia_sample(n=1):
def marsaglia():
while True:
w1 = (np.random.rand() * 2) - 1
w2 = (np.random.rand() * 2) - 1
s = w1 * w1 + w2 * w2
if s < 1:
t = math.sqrt((-2) * math.log(s) / s)
z1, z2= w1 * t, w2*t
return z1, z2
z1 = np.empty(n)
z2 = np.empty(n)
for i in range(n):
z1[i], z2[i] = marsaglia()
return z1, z2
def plot_marsaglia_sample():
nSimulation = 5000
rand = marsaglia_sample(nSimulation)
plt.subplot(131)
plt.hist(rand[0], bins=100)
plt.title('histogram(X)')
plt.subplot(132)
plt.hist(rand[1], bins=100)
plt.title('histogram(Y)')
plt.subplot(133)
plt.scatter(rand[0], rand[1])
plt.title('X vs Y')
plt.show()
if __name__ == '__main__':
plot_marsaglia_sample()해당 결과는 아래와 같습니다.
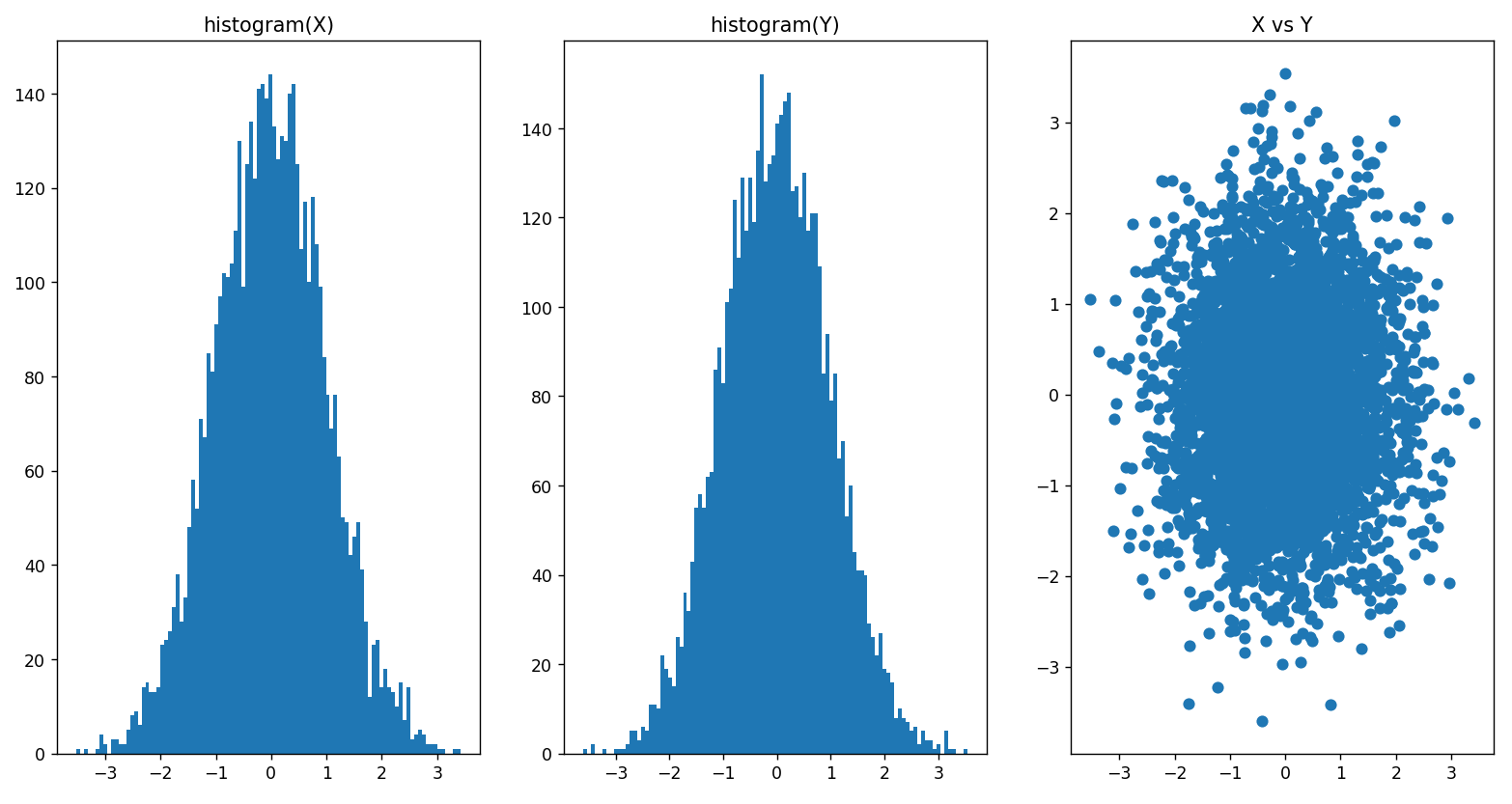
Box-Muller와 대동소이한 결론임을 확인할 수 있습니다. 그런데 왜 Marsaglia 방법은 Box-Muller에 비해 안 쓸까요?
$\sin$, $\cos$ 등 어려운 함수도 안 쓰는데요. 바로 계산 시간이 너무 느리기 때문입니다. 직접 python으로 비교해볼까요?
Box-Muller 와 Marsaglia Method 계산 시간 측정하기
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import time
if __name__ == '__main__':
nSimulation = 10000000
stime = time.time()
box_muller(nSimulation)
elasped_time1=time.time()-stime
stime = time.time()
marsaglia_sample(nSimulation)
elasped_time2 = time.time() - stime
print('Calculation time for box_muller is {}'.format(elasped_time1))
print('Calculation time for marsaglia is {}'.format(elasped_time2))code를 간략히 살펴보겠습니다.
import time시간을 측정하기 위해서는 time 이라는 모듈이 필요합니다.
stime = time.time()
box_muller(nSimulation)
elasped_time1=time.time()-stimetime.time()을 사용하여 현재 시점을 측정하고, 계산이 끝난 후 time.time()과의 차이를 계산하여 계산시간을 측정합니다.
결과를 보실까요?
Calculation time for box_muller is 1.5565705299377441
Calculation time for marsaglia is 22.14859962463379
Process finished with exit code 0Marsaglia 방법이 무려 15배 가까이 시간이 오래 걸리네요! 왜 그럴까요?
답은 $ x^2+y^2\leq 1$을 만족하는 $[-1,1]$구간의 난수를 찾는데 시간이 많이 걸리기 때문입니다. 위의 [그림1]의 원과 정사각형의 관계에서
- $[-1,1]$사이의 난수 $x,y$선택은 정사각형에 해당
- $x^2+y^2\leq 1$은 원에 해당
합니다. 따라서 기하학적인 확률로 봤을 때 정사각형의 넓이만큼 에서 원의 넓이만큼이 난수 추출 성공이죠.(나머지는 버립니다.)
즉,
$$ \frac{\pi}{4}$$
만큼이 성공이죠. 이렇게 버려지는 부분이 있어서 계산시간이 오래 걸리는 것이고, 따라서 Marsaglia 대신 Box-Muller 방법을 쓰는 것입니다.
지금까지
| 방법1 | 중심극한 정리를 이용하여, uniform random number의 표본평균 구하기 |
| 방법2 | Normal cumulative distribution function 을 이용하기 |
| 방법3 | Box Muller 방법으로 정규분포 난수 2개를 한방에 구하기 |
에 대해서 알아봤는데요. (상기의 이유로 Marsaglia는 뺐습니다.)
그럼 방법 1,2,3 중 가장 좋은 방법은 무엇일까요? 다음 글에서 알아보도록 하겠습니다.
'수학의 재미 > 확률분포' 카테고리의 다른 글
| 무엇이 더 정규분포인가? Jarque-Bera Test (0) | 2022.06.17 |
|---|---|
| 정균분포 난수를 만들어 주세요 #6 : random.normal (0) | 2022.06.17 |
| 정균분포 난수를 만들어 주세요 #4 : Box-Muller 방법 (0) | 2022.06.15 |
| 정균분포 난수를 만들어 주세요 #3 : Normal CDF 이용 (0) | 2022.06.14 |
| 정균분포 난수를 만들어 주세요 #2 : Normal CDF 이용 (0) | 2022.06.13 |




댓글