정균분포 난수를 만들어 주세요 #4 : Box-Muller 방법

이번 글은 

2022.06.14 - [수학의 재미/확률분포] - 정균분포 난수를 만들어 주세요 #3 : Normal CDF 이용

정균분포 난수를 만들어 주세요 #3 : Normal CDF 이용

에서 이어집니다. 정규분포 난수를 구하는 가장 유명하고 아름다운 방법입니다.

방법1	중심극한 정리를 이용하여, uniform random number의 표본평균 구하기
방법2	Normal cumulative distribution function 을 이용하기
방법3	Box Muller 방법으로 정규분포 난수 2개를 한방에 구하기

Box 와 Muller는 각각 통계학자, 컴퓨터 과학자입니다.

호..혹시 박스 뮬러? Franck Muller unveils the First Automated Watch Box - Watch I Love

어떠한 식으로 정규분포 난수를 얻어내는지 그 테크닉을 감상하시죠.

문제는 

$$ I=\int_{-\infty}^{\infty} e^{-x^2/2}dx \tag{1}$$

의 값을 구하는데서 힌트를 얻습니다. 우선 식(1)을 어떻게 구하는지 알아봅니다.

이 값은 직접적인 적분으로 얻을 수 없다는 것이 알려져 있습니다. 대신 유명한 트릭으로 해결합니다.

$$
\begin{align}
I^2 & = \int_{-\infty}^{\infty} e^{-x^2/2}dx \cdot   \int_{-\infty}^{\infty} e^{-y^2/2}dy \cdot \\
      & =  \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2+y^2)/2} dxdy \\
     & = \int_0^{2\pi} \int_0^\infty e^{-r^2/2} rdr d\theta\\
    & = 2\pi \left[ -e^{-r^2/2}\right]_0^{\infty}\\
   & = 2\pi 
\end{align}
$$

중간에 

$$ x= r\cos\theta , y=r\sin\theta \tag{2}$$

극좌표계로 치환하는 방법이 쓰였습니다. 이렇게 되면 면적소 $dxdy$는 $r dr d\theta$로 바뀌게 됩니다.

결론적으로 

$$ I = \sqrt{2\pi}$$

이고

$$ 1= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \frac1{2\pi} e^{-(x^2+y^2)/2} dxdy $$

를 만족합니다.

Box Muller 방법은 바로 여기서 힌트를 얻는 것입니다.

우선 독립인 두 표준정규분포 $X,Y$의 joint probability density function은 

$$ f(x,y) = \frac1{2\pi} \exp\left( -\frac{x^2+y^2}{2} \right) $$ 입니다.  

따라서 어떠한 $(x,y)$에 대한 2차원 영역 $\mathcal{D}$에 대해 

$$\mathbb{P}(\mathcal{D}) = \iint_{\mathcal{D}} f(x,y)dxdy \tag{3}$$

입니다.

그러면 극좌표변환 식(2)를 사용하여 $\mathcal{D}$는 $(r,\theta)$에 대한 2차원 영역 $\mathcal{D}'$에 대응이 될 것이고,  수식(3)은

$$ \iint_{\mathcal{D}'} \frac1{2\pi} r e^{-r^2/2} drd\theta \tag{4} $$

라 치환이 됩니다.

그런데 수식(4)의 적분 되는 함수를 잘 살펴보면

$$ \frac1{2\pi} r e^{-r^2/2}$$

는 $(r,\theta)$의 joint probability density function (이것을 $f_{R,\Theta}$라 쓰죠.)이고 $R$의 density function $f_R$과 $\Theta$의 density function $f_{\Theta}$는 각각

$$ f_R(r) = re^{-r^2/2} ~,~ f_\Theta(\theta) = \frac{1}{2\pi}$$

라 쓰인 것이다!라고 해석이 됩니다. 심지어

$$ f_{R,\Theta}(r,\theta) = f_R(r) f_\Theta(\theta) $$

처럼 joint density function이 각각 density function의 곱으로 나눠지니 $R$과 $\Theta$의 independance도 보장이 됩니다.

 

또한 $0\leq r~,~ 0\leq \theta \leq 2\pi$ 임을 고려하여 $f_R$과 $f_{\Theta}$의 cdf  $F_R$과 $F_{\Theta}$를 구하면 각각

$$
\begin{align}
F_R(r) &= \int_0^r f_R(s) ds = \int_0^r se^{-s^2/2} ds =1-e^{-r^2/2} \\
F_{\Theta}(\theta) & = \int_0^{\theta} \frac{1}{2\pi} dt = \frac{\theta}{2\pi}
\end{align}
$$ 

이죠. 

여기서 마지막 단계로 또 cdf의 역함수 전법을 씁니다. 

uniform random number를 $w,v\sim \mathcal{U}[0,1]$ 2개 뽑습니다. 그리고

$$F_R(r) = w~, F_\Theta(\theta) =v$$

인 $r, \theta$를 찾으면 각각

$$ r= \sqrt{-2\ln(1-w)}~,~ \theta = 2\pi v$$ 가 되죠. 기호의 편의를 위해 $1-w:=u$로 바꾸면 $u$역시 uniform random이 될 것이고

$$ r= \sqrt{-2\ln u}~,~ \theta= 2\pi v$$

최종적으로 정리하면 다음의 결과를 얻습니다.

Box Muller Method
균등분포 난수 $u,v \sim \mathcal{U}[0,1]$를 뽑아
$$ x= \sqrt{-2\ln u} \cos(2\pi v) ~,~ y=\sqrt{-2\ln u} \sin(2\pi v) $$
라 하면 $x,y$는 서로 독립이고, 표준정규분포 $\mathcal{N}(0,1)$을 따른다.

위 정리가 표준정규분포 난수를 추출하는 가장 아름답고 효율적인 이론인 듯합니다.

 

coding을 해봅시다.

import math
import numpy as np
import matplotlib.pyplot as plt

def box_muller(n=1):
    u = np.random.rand(n)
    v = np.random.rand(n)

    r = np.sqrt(-2 * np.log(u))
    x = np.cos(2 * np.pi * v)
    y = np.sin(2 * np.pi * v)
    z1 = r * x
    z2 = r * y
    
    return z1, z2

if __name__ == '__main__':
    res= box_muller(3)
    print(res[0])

수식을 그대로 coding 해 주면 됩니다. 다만, 결괏값이 2개이므로 tuple 형식의 결과를 반환합니다.

결과는 아래와 같습니다.

[ 1.03447874 -0.66217353 -0.56004769]

Process finished with exit code 0

res[0]을 출력하므로 box_muller함수의 z1 이 출력되는 것입니다. 그렇다면 정말 정규분포 형태를 이루는지 관찰을 안 해볼 수 있겠죠. 3개 차트를 동시에 그려보겠습니다.

1. $X$좌표 (python code에서 z1) 을 뜻함
2. $Y$좌표 (python code에서 z2) 을 뜻함
3. $X$와 $Y$의 관계

import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

def box_muller(n=1):
    u = np.random.rand(n)
    v = np.random.rand(n)

    r = np.sqrt(-2 * np.log(u))
    x = np.cos(2 * np.pi * v)
    y = np.sin(2 * np.pi * v)
    z1 = r * x
    z2 = r * y
    return z1, z2

def plot_box_muller_result():
    nSimulation = 5000
    rand = box_muller(nSimulation)
    plt.subplot(131)
    plt.hist(rand[0], bins=100)
    plt.title('histogram(X)')
    plt.subplot(132)
    plt.hist(rand[1], bins=100)
    plt.title('histogram(Y)')
    plt.subplot(133)
    plt.scatter(rand[0], rand[1])
    plt.title('X vs Y')
    plt.show()

if __name__ == '__main__':
    plot_box_muller_result()

거두절미하고 결과를 보면,

 

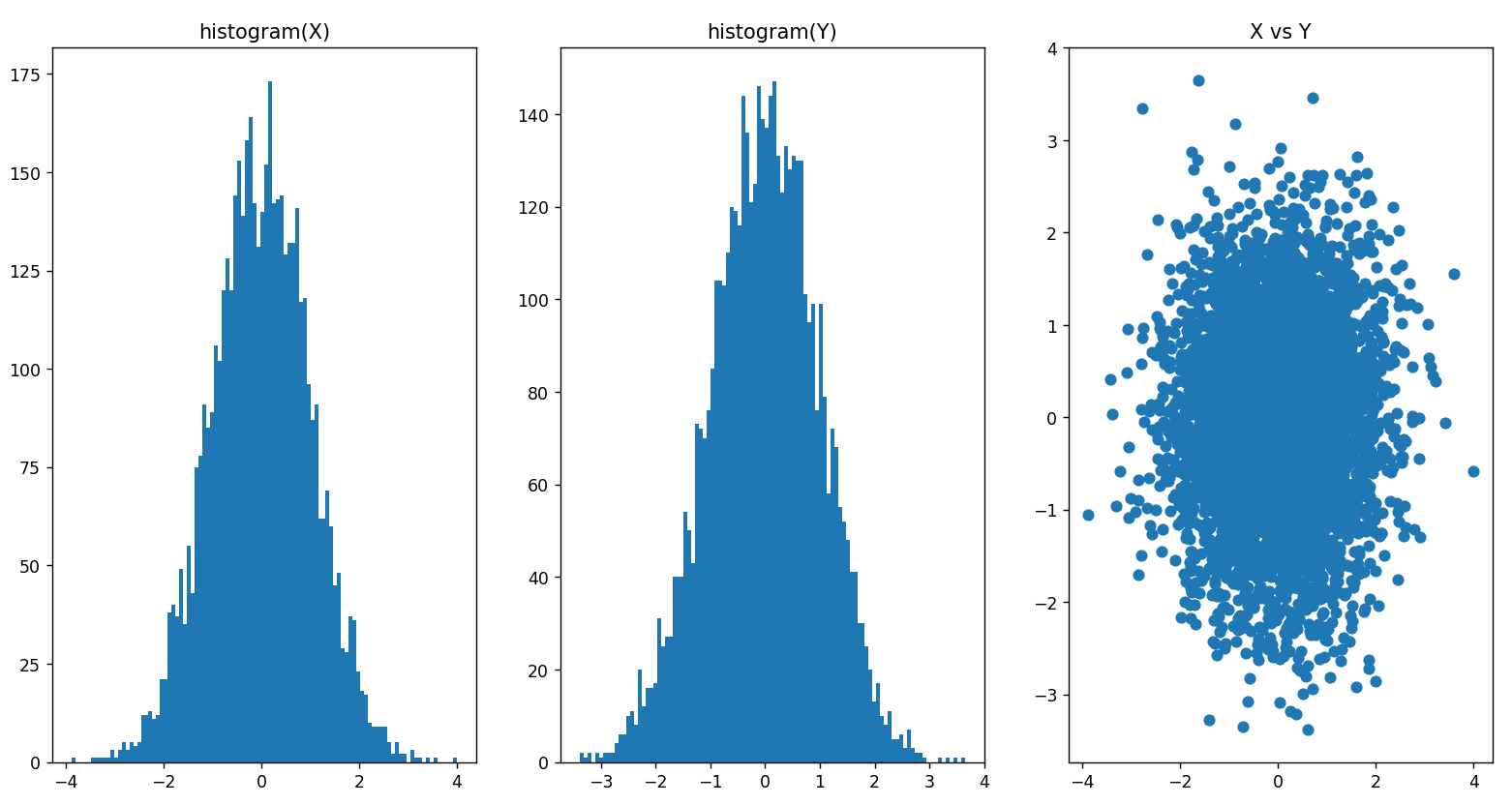
극좌표를 써서 $x,y$를 표현한 것이라, 관계는 세 번째 그림처럼 동그란 모양이 나옵니다. $x$와 $y$는 정규분포 양상을 띠고 있습니다. 

앞으로 이어질 글에서도 살펴보겠으나, Box Muller 방법은 정규성이 잘 보장되는 난수 발생 방법이라 많이 쓰입니다. 다음 글에서 조금 더 이야기를 진행해 보겠습니다.