2023.11.17 - [파이썬으로 풀어보는 고딩수학] - 프롤로그
프롤로그
살면서 참 수학이 본의 아니게 많이 쓰여. 중고딩 때는 그토록 어려웠던 수학이 생활 곳곳에서 사용되는 거 같아. 반면 다행인 것은 살면서 접하는 수학은 고등학교 수준 정도만 알고 있으면 충
sine-qua-none.tistory.com
위 글에서 말했다시피, 고등학교 수학문제들을 파이썬으로 풀어보는 게 목적이야.
평면좌표에서의 점, 직선, 원, 다각형 등 기하에 관련된 문제를 python으로 풀어볼 생각이지. 아래 문제를 먼저 풀어보자구
문제.
다음 세 점을 꼭짓점으로 하는 삼각형은 어떤 삼각형인가?
$$ A(1,4), B(-1,2), C(0,1)$$
우선 이 삼각형의 그림을 한번 그려볼게. python으로 다음과 같이 그릴 수 있지.
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
p1, p2, p3 = [1,4], [-1,2], [0,1] # 세 점
point_set = np.array([p1,p2,p3,p1]) # 세 점이 순환하도록 array를 만든다.
plt.xlim([-5,5])
plt.ylim([-5,5])
plt.plot(point_set[:,0], point_set[:,1]) # 점들의 x좌표, y좌표 array를 plotting한다.
plt.text(p1[0],p1[1], "A")
plt.text(p2[0],p2[1], "B")
plt.text(p3[0],p3[1], "C")
plt.axis('equal') # 정확한 모형을 보기 위해, 축의 scale를 equal로 둔다.
plt.show()
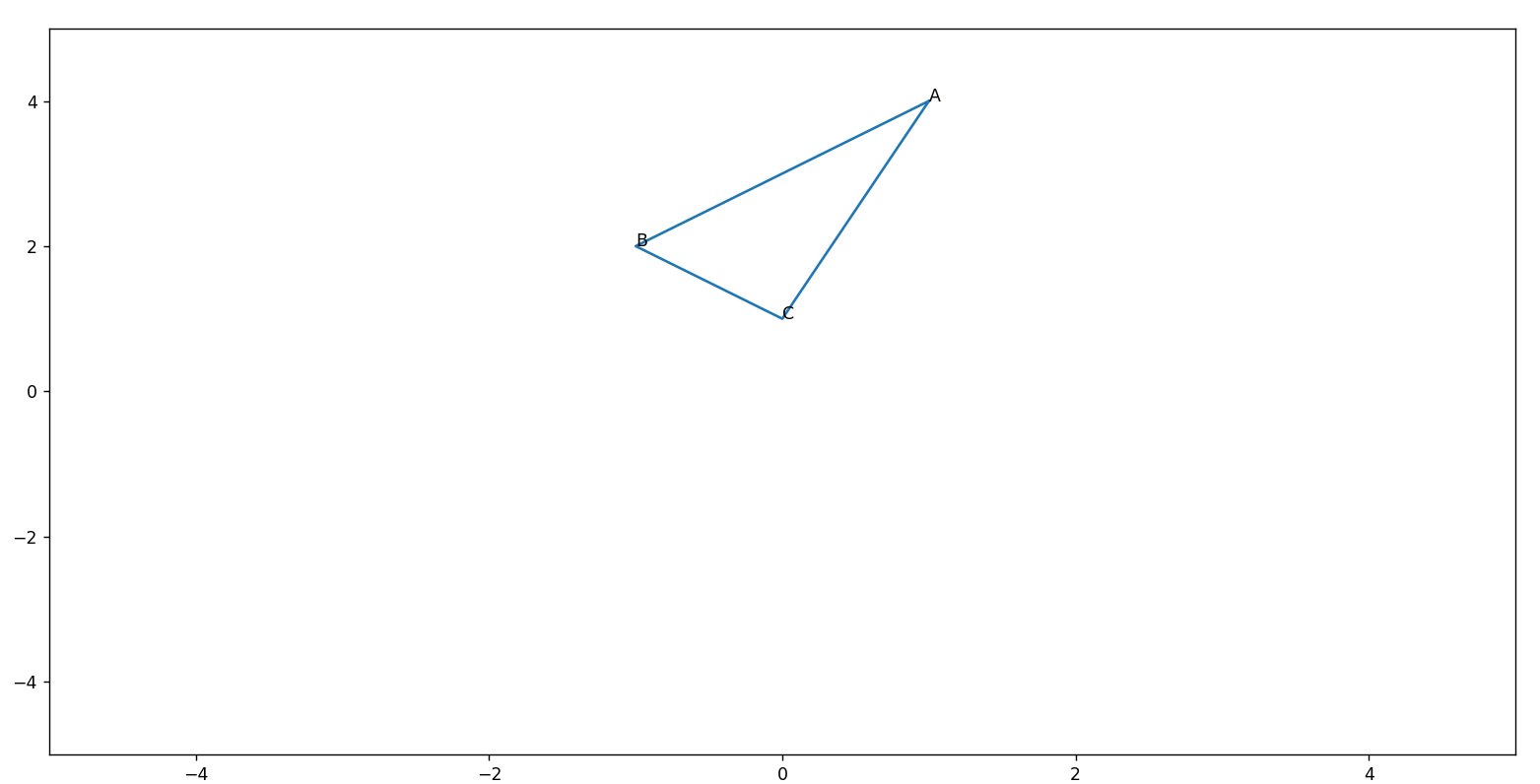
그러면 아래와 같이 삼각형의 그래프가 그려져(주의할 점은 세 점이 순환하도록 point_set이라는 array를 점이 순환하게 만들어 준 것!, 그래야 점들을 선으로 모두 연결하는 그래프가 나오지)

딱 보니까, 각 B가 직각인 직각삼각형으로 보이지 않나? B가 직각이라는데 내 돈 모두를 걸고 싶은 지경이야.
그런데 여기서 맹점 한 가지 알려줄게. 아래 더 보기를 봐봐
만일 위 코드에서
plt.axis('equal')
를 생략하면 어떻게 될까?
그래프 좀 봐봐. 같은 그래프인데, python matploblib에서 기본으로 제공하는 차트 $x, y$축 비율 때문에 삼각형이 왜곡 져 보여. 도저히 각 $B$가 직각이라는 사실을 알 수 없지.
따라서 이렇게 육안으로 판별할 때는, $x, y$축의 scale를 맞춰 주는 함수를 써 줘야 함!
자, 다시 돌아가서 $\angle B$가 직각이라는 합리적 의심을 어떻게 python으로 판단할 수 있을까?
is_right() 함수
python 내의 강력한 라이브러리인

를 쓸 거야. 중고딩 수학채에서 보던 $x, y$등 모든 변수, 그리고 변수와 관련된 함수 및 함수 분석 등 모두 sympy가 담당하지. 아래 나오는 함수(또는 객체)인 Triangle이나 Point, is_right() 함수 등은 모두 sympy 내에 이미 만들어져 있는 애들이야.
from sympy import *
p1, p2, p3 = Point([1,4]), Point([-1,2]), Point([0,1]) # 세 점을 Point 객체로 만든다.
tr = Triangle(p1, p2, p3) # p1,p2,p3를 꼭지점으로 하는 삼각형을 만든다.
print(tr.is_right()) # 삼각형 tr이 직각삼각형인지 판별함
위와 같이 sympy에 있는 모든 걸 import 하고 이걸 실행해 보면,
True
답이 True가 나오네. is_right 가 True라는 거야. right는 알다시피 수학용어로 쓰면 직각이라는 단어거든.
위의 code에 다음을 추가해 볼까? 각각의 각 들의 정확한 값을 알고 싶거든
ang_A, ang_B, ang_C = tr.angles[p1], tr.angles[p2], tr.angles[p3]
print( "Three angles : ")
print( f"angle A : {ang_A}")
print( f"angle B : {ang_B}")
print( f"angle C : {ang_C}")
참고로, 다각형의 각(angle)을 알고 싶을 때는 angles [pt]라는 함수를 쓰면 돼. 결과를 보면,
Three angles :
angle A : acos(2*sqrt(5)/5)
angle B : pi/2
angle C : acos(sqrt(5)/5)
간단히 수학 용어를 복습해 보면
| sympy 기호 | 수학적인 뜻 |
| acos | $\cos^{-1} $ 또는 $\arccos$ |
| pi | $\pi$, 원주율 |
| sqrt | $\sqrt{\cdot}$, 루트 |
따라서 저 결과에 따르면
$$ \cos A = \frac{2\sqrt{5}}{5} ~,~ \angle B = \frac{\pi}{2}~,~ \cos C = \frac{\sqrt{5}}5 $$
라는 얘기야
각들을 다 구해봤는데, 진짜 직각이 있네. is_right 하지!!
다른 삼각형 모양 판별법
sympy로는 직각삼각형뿐 아니라, 정삼각형이냐, 이등변 삼각형이냐 등도 따질 수 있어. 한번 보면,
print(f"Is equilateral ? :{tr.is_equilateral()}")
print(f"Is isosceles ? :{tr.is_isosceles()}")
를 추가해서 결과를 보면
Is equilateral ? :False
Is isosceles ? :False
equilateral, isosceles는 각각 정삼각형, 이등변삼각형 여부를 묻는 단어야. 해당 삼각형은 정삼각형도 아니요, 이등변 삼각형도 아니지.
이렇게 판단을 할 수 있는 거야.
sympy 함수 정리
위에서 썼던 sympy 함수들을 정리해 볼게
| 함수 | 뜻 |
| Point | 점(point), 점의 좌표를 list 형이나 tuple형으로 받는다. |
| Triangle | 삼각형을 정의함 |
| is_right | 직각삼각형이냐를 따지는 함수, True or False |
| is_equilateral | 정삼각형인지를 판단하는 함수, True or False |
| is_isosceles | 이등변 삼각형인지를 판단하는 함수, True or False |
유용하고 멋진 함수들이 많지. 이제 시작일 뿐이야~
'파이썬으로 풀어보는 고딩수학 > 평면좌표' 카테고리의 다른 글
| 파푸스의 중선 정리 with Sympy (0) | 2023.12.13 |
|---|---|
| 삼각형의 무게중심을 sympy로 구하기 (0) | 2023.12.06 |
| 직각삼각형 만들기 (0) | 2023.12.01 |
| 삼각형의 외접원 구하기 (0) | 2023.11.29 |
| 두 점에서 거리가 같은 직선상의 점 구하기 (0) | 2023.11.28 |




댓글