Brownian bridge: 1년뒤 주가타겟을 정조준하는 일일주가의 움직임을 모델링하자 #1

 

이번 글은 지수/주가 모델링 중 유용한 테크닉으로 알려진 브라운 브리지(Brownian bridge)에 대해 알아보려 합니다.

Brown 운동은 위너 프로세스(Wiener process)로도 잘 알려져 있으며, 지수/주가 모델 중 GBM 모델을 설명하는데 긴요하게 쓰입니다. 

주가를 $S_t$라 했을 때, GBM 은 

$$dS_t/S_t = (r-q)dt + \sigma dW_t$$

형태의 다이나믹을 가집니다. 여기서 $W_t$는 위너 프로세스입니다. 이토의 렘마를 이용하여 이를 풀면 미래의 특정 시점 $T$에 대해

$$S(T) =S(0) \exp\left( (r-q-\textstyle{\frac12}\sigma^2)T +\sigma \sqrt{T} z\right)\tag{1}$$

식으로 쓸 수 있습니다. 여기서 $z$는 표준 정규분포 난수입니다.

 

따라서 미래 시점 $T$에 기대되는 주가 $S(T)$를 산출하기 위해서 난수 $z$를 계속 뽑아가며, 가능할 법한 $S(T)$들을 뽑아냅니다. 이 자료를 바탕으로 미래를 예측해 보는 것이죠.

 

식(1)을 이용하여 현재가 $S(0)=100$인 상태에서 1년 뒤, 즉, $T=1$에서의 예상 주가들을 20개만 뽑아내면 아래 그림처럼 분포할 것입니다(무위험 이자율 2%, 주식의 변동성 30% 가정, 배당은 없음)

 

GBM하에서 기대되는 예상 만기주가의 분포 모습

 

이렇게 1년 뒤의 주가 분포를 예측해 볼 수 있는데요. 1년 동안 주가가 어떻게 흘러서 저런 예측값들이 나왔는지 궁금할 경우가 있습니다. 요즈음은 금융 상품 구조나 거래의 조건이 복잡해지면서, 만기 주가 상태뿐이 아닌, 만기까지 어떻게 흘러왔는지를 따져 볼 필요가 생겼거든요. 예를 들어 아래 그림과 같이 특정 타깃에 어떻게 도달했는지를 이론적으로 알아볼 필요가 있는 것이죠.

 

 

 

일례로, 아래 그림처럼 도달했을 수 있습니다.

 

 

특히 스텝다운 ELS처럼 조기/만기 상환의 위치가 제일 중요한데, 조기/만기 상환이 안될 경우 데일리로 낙인을 쳤는지 여부를 따져야 하는 상품들을 모델링할 때, 이런 니즈가 필요하겠죠.

 

이렇게 특정 종착역(위 그림에서는 시작점인 $S(0)$와 끝점인 $S(T)$) 두 개를 잇는 패스를 생성하는 과정을 마치 다리를 놓는 과정처럼 보인다 해서 bridge라는 용어를 쓰고, Brownian 운동(위너프로세스)으로 주가는 움직여야 하므로 이를 합쳐서

브라운 브리지(Brownian Bridge)

라 합니다.

 

 

이제 위의 다리를 어떻게 건설하는지 알아보겠습니다.

 

 

Brownian Bridge 설계

 

미래의 한 시점을 $T$ 라 합시다.

위너 프로세스 $Z(t)$에 대해 $Z(0)$이 시작 역, $Z(T)$가 종착역이라 합시다. 이 두 값은 이미 결정된(알려진) 값들이라 합시다. 가장 어설픈 다리는 아래와 같이 선형으로 다리를 연결해 보는 것입니다.

 

 

시간축과 난수 축 2차원 평면에서 $(0,Z(0))$ 과 $(T,Z(T))$를 연결하는 직선은 

$$y= \frac{Z(T)-Z(0)}{T} x + Z(0)$$

입니다. $Z$가 위너 프로세스이므로 $Z(0)=0$ 이 되고요. 따라서 시점 $t$에서의 값은

$$\frac{t}{T}Z(T)$$

입니다. 이 친구를 브라운 브리지라고 우겨 볼 수 있겠죠. 얘를 $B(t)$라 해봅시다. 즉,

$$B(t) = \frac{t}{T}Z(T)\tag{2}$$

라 합시다.

 

이왕 만드는 김에, $B(t)$를 위너 프로세스로 만들고 싶습니다.  과연 $B(t)$는 위너프로세스일까요?

$B(t)$가 위너프로세스라면, $\mathbb{E}(B(t)^2) =t$ 여야 할 것입니다. 분산이 $t$이기 때문이죠. 

 

그런데 식(2)의 우변을 제곱하여 기댓값을 구하면

$$\mathbb{E}\left(\frac{t^2}{T^2}Z(T)^2 \right) = \frac{t^2}{T^2} T = \frac{t^2}{T}$$

가 나와서 성립하지 않습니다. 

 

약간의 보정을 해보죠. 식(2)의 우변에

$$W(t) - \frac{t}{T} W(T) \tag{3}$$

를 더해봅시다. 여기서 $W(t)$은 기존의 $Z(t)$와 독립인 또 다른 위너프로세스입니다.

 

식(3)은 다음과 같은 특징이 있습니다. $t=0$을 대입하면 준식은 0입니다. $t=T$를 대입해도 0이 나오죠. 따라서 식(3)은 0과 0을 연결하는 또 하나의 다리인 셈입니다.

 

0과 0을 연결하는 다리(bridge) 프로세스

 

 

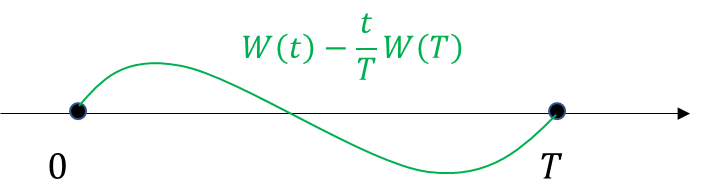
이제 식(2)을 다음과 같이 세팅합니다.

 

$$B(t) = \frac{t}{T} Z(T) + W(t) -\frac{t}{T}W(T) \tag{4}$$

 

 

그럼 $B(t)$는 위너프로세스가 될까요? 우선 모든 $t$에 대해 평균이 0인 정규분포임은 확실합니다. $Z(T), W(t), W(T)$의 1차 결합으로 이루어져 있으니 당연히 정규분포이고, 각각의 평균이 0이니 일차 결합한 값도 0이죠.

 

분산을 구하기 위해 2차 모멘텀인 $\mathbb{E}(B(t)^2)$의 값을 계산해보겠습니다.

$$B(t)^2 = \left(\frac{t}{T}\right)^2 Z(T)^2 + 2 \frac{t}{T}Z(T) \left(W(t)-\frac{t}{T}W(T)\right) + \left(W(t)-\frac{t}{T}W(T)\right)^2$$

 

여기에 기대값 $\mathbb{E}(\cdot)$를 취해볼까요.

첫 번째 항은 $Z(T)^2$의 기댓값이 $T$ 임을 이용하면 $\frac{t^2}{T^2} \cdot T = \frac{t^2}{T}$ 를 얻습니다.

두 번째 항은 $Z(T)$와 $W(\cdot)$가 독립임을 이용하면 곱하기가 서로 분리되어 기댓값이 취해지므로 0을 얻죠.

세 번째 항은

$$\begin{align} \mathbb{E}\left(W(t)-\frac{t}{T}W(T)\right)^2 &= \mathbb{E}(W(t)^2) -2\frac{t}{T}\mathbb{E}(W(t)W(T)) +\frac{t^2}{T^2}\mathbb{E}(W(T)^2)\\ & = t + \frac{t^2}{T} -2\frac{t}{T}\mathbb{E}(W(t)W(T)) \\ & =  t + \frac{t^2}{T} -2\frac{t}{T}\cdot t \\ & = t - \frac{t^2}{T} \end{align}$$
입니다. 위 등식의 세 번째 등식은
$$\mathbb{E}(W(t)W(T)) =\mathbb{E}(W(t)(W(T)-W(t)) + \mathbb{E}(W(t)^2) =\mathbb{E}(W(t)) \mathbb{E}(W(T)-W(t)) +t =t$$
가 나옵니다. 위너프로세스의 정의에 의해 $W(t)$와 $W(T)-W(t)$가 독립이기 때문이죠.

 

따라서 정리하면

$$\mathbb{E}(B(t)^2) = \frac{t^2}{T} + t-  \frac{t^2}{T} = t$$  

를 얻었습니다. 즉, $B(t)$의 분산은 $t$라은 얘기가 됩니다.

 

따라서  $B(t)$가 위너프로세스가 됨을 알 수 있습니다(물론 위너프로세스를 엄밀하게 증명하는 방법은 아닙니다.)

 

 

 

일반적인 Brownian Bridge

 

위의 경우는 한 시점이 $0$인 경우를 가정했습니다.  그러면 만일 일반적인 시점 $T_1$과 $T_2$를 연결하는 다리는 어떻게 될까요?

$T_1$ 시점에 위너프로세스가 $Z(T_1)$이고, $T_2$ 시점에 $Z(T_2)$로 미리 결정되어 있다고 가정을 해보겠습니다.

 

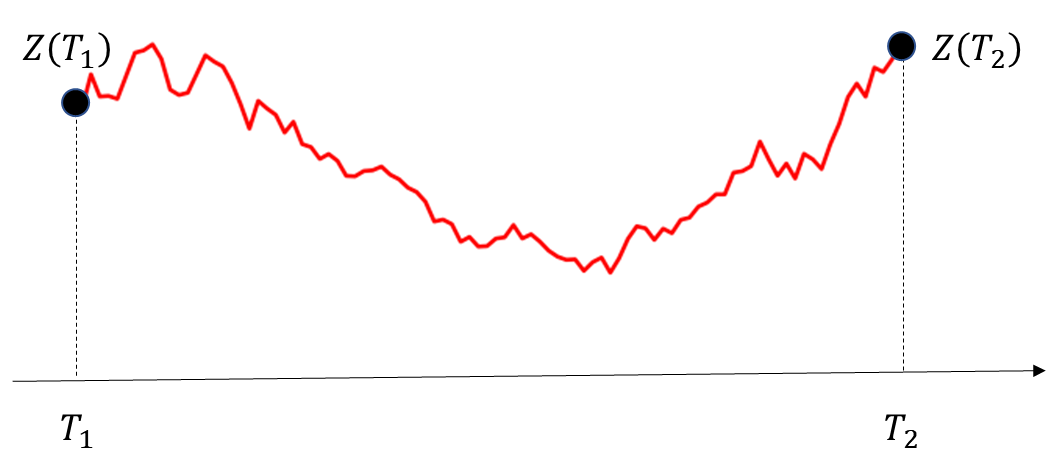
위 그림에서 빨간 선처럼 위너 프로세스로 다리를 연결하려면 어떻게 할까요?

 

식 (4)의 원래 숨은 뜻은

$$B(t) = Z(0) + \frac{t}{T} (Z(T)-Z(0)) + W(t) -\frac{t}{T}W(T)$$

였는데요, 이것을 자연스럽게 확장하면 됩니다.
이제 $t$은 $T_1$과 $T_2$사이의 시점이 되는 것이고, $0\mapsto T_1~,~ T\mapsto T_2$인 상황이죠.
그럼 만기는 $T \mapsto T_2-T_1$ 에 대응될 거고요. 마지막으로
$$t \mapsto t-T_1$$
에 대응될 것입니다. 따라서 다음처럼 Brownian Bridge를 건설하면 됩니다.

 

Brownian Bridge 일반 버전

$T_1<=t<=T_2$ 인 시점 $t$에 대해, $$B(t) = Z(T_1) + \frac{t-T_1}{T_2-T_1} (Z(T_2)-Z(T_1)) + W(t-T_1) - \frac{t-T_1}{T_2-T_1} W(T_2-T_1)$$

 

이제 Brownian bridge의 원리를 알았습니다. 그러면 이를 이용하여 어떻게 주가 패스를 생성할 수 있는지 다음 글에서 다뤄보도록 하겠습니다.

 

제가 본 다리중 가장 웅장했던 보스포러스 대교(튀르키에)