파생상품의 양대 축은
1. Equity를 기초자산으로 하는 상품
2. 금리를 기초자산으로 하는 상품
입니다. 더 깊게 들어가 보면, 신용이나 상품(commodity)을 기초자산으로 하는 상품도 상당히 큰 비중을 차지하고 있지만, Equity에 비견될 것으로는 아무래도 금리이겠죠.
이번 글에서는 금리에 대해 다뤄보도록 하겠습니다.
금리란?
생활을 영위하거나 투자를 위해 우리는 돈을 조달하게 됩니다. 하지만 돈을 공짜로 빌려주는 사람은 없겠죠. 돈을 빌려주는 사람 입장에서는 자기가 그 돈으로 수익활동을 얻게 되는 기회를 놓쳐버리니까요. 이른바 기회비용이죠.
따라서 돈을 빌려주는 대신, 얼마만큼이 보상을 받게 되는데, 이를 이자라고 합니다. 상황이 급박한 사람들에게 돈을 빌려줄 때는, 보상(이자)을 크게 받아도 됩니다. 또 믿을 만한 구석이 떨어지는 사람에게도 더 많은 보상(이자)을 요구할 수 있습니다. 나 말고 다른 누군가에게 돈을 빌리기가 힘들기 때문이죠.
이자는 보통 연단위로 표시합니다. 전세담보대출 4%로 1억을 받았다면, 전세 2년 동안 800만 원의 이자를 지불한단 뜻이죠. 1년에 4% 즉, 400만 원이니깐요.
이자계산방법에는 단리와 복리가 있습니다. 단리는 원금에 대한 이자만 발생하고, 복리는 원금과 그간 발생한 이자를 합한 것에 또 이자가 붙어 나가는 원리입니다.
우리가 돈을 빌리고, 이자를 복리로 낸다는 가정은 좀 서러우니, 우리가 돈을 빌려주는 상황을 가정해 봅시다.
우리가 은행에 돈을 빌려준다고 합시다. 다른 말로 예금에 가입하는 거죠.
우리가 이자를 받는 방법은 크게 단리와 복리가 있습니다. 영어로는 각각 simple interest, compound interest 입니다. 말 그대로, 단리는 단순한 방법의 이자, 복리는 복잡한 방법의 이자이죠.
단리
만일 연이자율 $r$로 $n$년 동안 $N$원을 묵혀두면 $n$년 뒤에는
$$ N(1+n\cdot r)$$
이 원리합계가 됩니다. (원리합계는 원금과 이자의 합계라는 뜻입니다.)
위의 그림을 보시죠. 만일 원금을 1원이라 하면 연간이자는 $r$원이 됩니다. 이것이 연간으로 계속 들어오는 것입니다. 만일 10년이면, 이자의 합계는 $10r$이 되고, 일반적으로 $n$ 년이면
$$n\cdot r$$
이 되죠. 따라서 $n$ 년 뒤의 원리 합계는
$$ 1+ n\cdot r$$ 이 되고, 일반적으로 원금이 $N$원이면,
$$ N(1+n\cdot r)$$
이 되는 것입니다.
1년 복리
이번엔 복리에 대해 살펴보겠습니다. 복리는 원금에 그간 누적된 이자까지 더한 것을 새로운 원금으로 보고 거기에 원금이 붙는 원리입니다. 원금이 계속 늘어나니 이자도 늘어나고, 암튼 쉬운 말로 그간 발생한 이자에도 이자가 붙는다는 ㅐ념입니다. 원금이 계속 불어나는 형태이니 단리보다 유리할 수 있죠. 1년에 한 번씩 이자율 $r$로 이자가 붙는다고 가정합시다.
이 때는
$$ N \left( 1+ r \right)^n $$
이 원리합계가 되겠죠. 그 이유는 아래의 그림에서 확인 가능합니다.
이자 산정 대상이 되는 원금이 1년, 2년 지날수록 계속 증가하는 상황이고, 그 증가율이 바로 $1+r$이 됩니다.
반년 복리
이번엔 이자가 반년에 한번씩 발생한다고 해 봅시다. 연이율 $r$로 공표한 예금은 반년에 $\frac{r}{2}$ 의 이자율만큼 준다는 뜻입니다. 이자를 받을 기회는 $2n$번이 되고요.
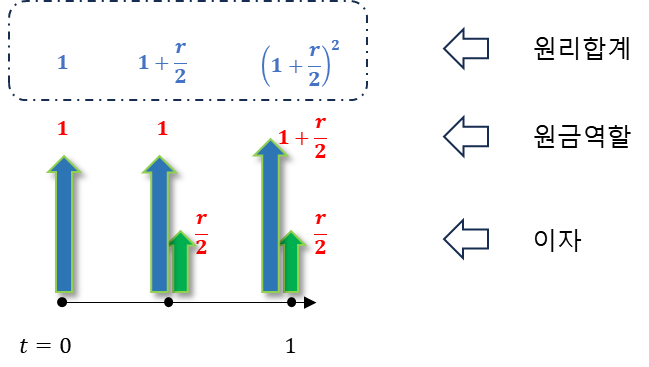
따라서 원리합계는
$$ N \left( 1+ \frac{r}{2} \right)^{2n} $$
가 됩니다.
분기복리
분기 복리는 분기에 한 번씩 이자를 지급한다는 뜻입니다. 분기별로 $\frac{r}{4}$를 받는 예금이고 이자 쌓이는 기회는 $4n$번이 있지요. 따라서
$$ N \left( 1+ \frac{r}{4} \right)^{4n} $$
이 됩니다.
월복리
월마다 복리로 이자를 주는 상품도 있습니다. 월별로 $\frac{r}{12}$만큼의 이자율을 받을 거고, 기회는 $12n$번이 있습니다. 따라서
$$ N \left( 1+ \frac{r}{12} \right)^{12n} $$
연속복리
이제 매시각, 매분, 매초, 그 보다 더 짧은 주기의 복리로 불어나는 상황을 가정해 보죠.
주기가 짧아진다, 즉, 이자 주는 지급주기가 연속적으로 일어난다고 생각해 보는 것입니다. 만일 연간 $m$번을 지급하는 주기라면
매번 주는 금리는
$$ \frac{r}{m}$$이 되고, 연간 $m$번 주므로 $n$년 동안은 $mn$번 주는 셈이 됩니다. 이 때 원리합계는
$$ N \left( 1+ \frac{r}{m} \right)^{mn} $$
이 됩니다. 만일 $m$을 무한대로 보면 어떻게 될까요?
$$ \lim_{m\rightarrow \infty}N \left( 1+ \frac{r}{m} \right)^{mn} = \left(\lim_{m\rightarrow \infty}N \left( 1+ \frac{r}{m} \right)^{m} \right)^n = (e^{r})^n = e^{rn}$$
이 됩니다.
즉, 이자지급주기를 무한대로 쪼개면, 다시 말해 이자지급을 연속적으로 복리 방법으로 주면 $n$년 동안의 원리하계는
$$ e^{rn}$$
이 되는 것입니다.
각 이자지급 방법별 원리합계 비교
python으로 단리(simple rate), 여러 가지 복리(compund rate) 그리고 연속복리(continuous compound rate)의 원리합계를 비교해 보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
rate = 0.05 # 이자율 5% 로 가정
freq = np.array([1, 2, 3, 4, 6, 12, 182, 365]) # 연간 지급횟수, 1번, 2번, 3번..., 365번
comp_principal_sum = (1 + 0.05 / freq) ** freq
simple_principal_sum = 1 + rate
conti_principal_sum = np.exp(rate)
plt.plot(freq, comp_principal_sum, 'o-', label='compound rate')
plt.hlines(simple_principal_sum, xmin=freq[0], xmax=freq[-1], color='r', label='simple rate')
plt.hlines(conti_principal_sum, xmin=freq[0], xmax=freq[-1], color='g', label='continuous rate')
plt.legend()
plt.show()
코드 중간의 계산식들은 위의 설명을 참고하시기 바랍니다. 결과는
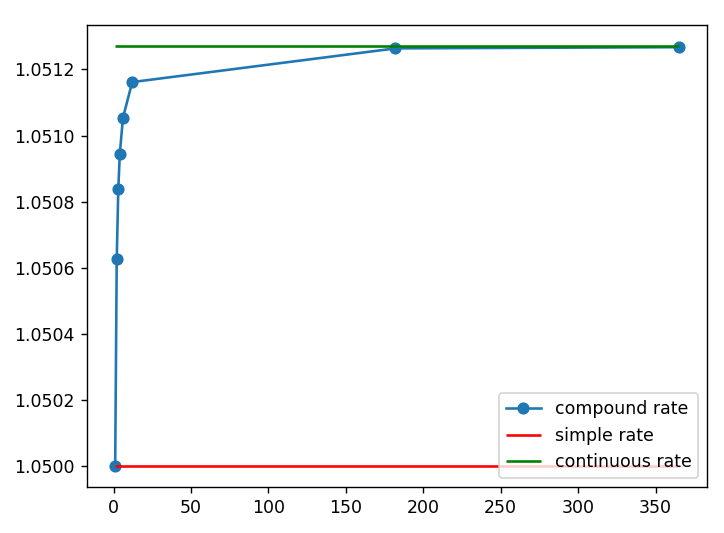
이자율이 같은 때에는 복리가 매력 있겠죠? 궁극적으로 연속복리의 원리합계가 가장 높겠지만, 현실적으로는 연속으로 복리를 챙겨준다는 것은 불가능합니다.
연속복리는 금융공학의 할인율을 계산할 때 많이 쓰이게 됩니다.
댓글