지난 글에서 우리는 파푸스의 정리를 다뤘었지. 파푸스의 중선 정리 with Sympy
파푸스의 중선 정리 with Sympy
전 글 삼각형의 무게중심을 sympy로 구하기 삼각형의 무게중심을 sympy로 구하기 직각삼각형 만들기 직각삼각형 만들기 이번 글은 삼각형의 외접원 구하기 삼각형의 외접원 구하기 저번 글 두 점
sine-qua-none.tistory.com
위 글의 말미에 스튜어트 정리라는 것을 소개한 바 있어. 스튜어트 정리는 파푸스 정리의 일반화된 정리이지. 위키피디아에도 소개가 되어 있지만, 여기서 다시 소개를 해 볼게.
스튜어트 정리

스튜어트 정리란? 위의 그림에서
$$m \cdot b^2 + n\cdot c^2 = a(d^2 + m\cdot n)\tag{1}$$
를 뜻하지. 특별히 $X$가 변 $BC$의 중점인 경우, 즉
$$ m=n=a/2$$
인 경우, 식(1)은
$$ m \cdot b^2 + m\cdot c^2 = 2m (d^2 + m\cdot m)$$
이므로 $m$을 약분하여 파푸스 정리를 얻을 수 있어.
자, 이 정리를 python으로 접근할 수 있는지 한번 볼게
Python Code (지저분한 결과)
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
x1, x2, x3 = symbols("x1 x2 x3")
y1, y2, y3 = symbols("y1 y2 y3")
t = symbols("t") # X를 매개변수(t)로 표현하기 위한 symbol t 정의'
A, B, C = Point(x1, y1), Point(x2, y2), Point(x3, y3) # 점 A,B,C
X = Segment(B, C).arbitrary_point(t) # 선분 BC위의 임의의(arbitraty) 점을 나타냄
a = B.distance(C) # BC의 길이
b = A.distance(C) # AC의 길이
c = A.distance(B) # AB의 길이
d = A.distance(X) # AX의 길이
m = B.distance(X) # BX의 길이
n = C.distance(X) # CX의 길이
eqn1 = b ** 2 * m + c ** 2 * n # 스튜어트 정리의 좌변(LHS)
eqn2 = a * (d ** 2 + m * n) # 스튜어트 정리의 우변(RHS)
eqn1 = eqn1.doit() # LHS 계산
eqn2 = eqn2.doit() # RHS 계산
eqn1 = eqn1.expand() # 전개할 수 있으면 LHS 전개하여 정리
eqn2 = eqn2.expand() # 전개할 수 있으면 RHS 전개하여 정리
print('LHS of Stewart Theorem')
print(eqn1)
print('RHS of Stewart Theorem')
print(eqn2)
print(f'Is Stewart Theorem true? {eqn1 == eqn2}') # 좌변과 우변은 같나?
위의 코드는 삼각형 $ABC$의 점을 임의의 점을
$$ A(x_1,y_1) ~,~ B(x_2, y_2)~,~ C(x_3,y_3)$$
와 같이 symbols을 써서 표현한 뒤,
$BC$위의 임의의 점을 arbitrary_point라는 함수를 사용하여 매개변수 $t$로 나타내고,
스튜어트 정리의 좌변, 우변을 무작정 구해본 것이야.

결과를 보자고
LHS of Stewart Theorem
x1**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2) + x1**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2 - 2*t*x2**2 + 4*t*x2*x3 - 2*t*x3**2 - 2*t*y2**2 + 4*t*y2*y3 - 2*t*y3**2 + x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*x1*x2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2 - 2*t*x2**2 + 4*t*x2*x3 - 2*t*x3**2 - 2*t*y2**2 + 4*t*y2*y3 - 2*t*y3**2 + x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*x1*x3*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2) + x2**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2 - 2*t*x2**2 + 4*t*x2*x3 - 2*t*x3**2 - 2*t*y2**2 + 4*t*y2*y3 - 2*t*y3**2 + x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + x3**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2) + y1**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2) + y1**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2 - 2*t*x2**2 + 4*t*x2*x3 - 2*t*x3**2 - 2*t*y2**2 + 4*t*y2*y3 - 2*t*y3**2 + x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*y1*y2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2 - 2*t*x2**2 + 4*t*x2*x3 - 2*t*x3**2 - 2*t*y2**2 + 4*t*y2*y3 - 2*t*y3**2 + x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*y1*y3*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2) + y2**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2 - 2*t*x2**2 + 4*t*x2*x3 - 2*t*x3**2 - 2*t*y2**2 + 4*t*y2*y3 - 2*t*y3**2 + x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + y3**2*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2)
RHS of Stewart Theorem
t**2*x2**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*t**2*x2*x3*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + t**2*x3**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + t**2*y2**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*t**2*y2*y3*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + t**2*y3**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + 2*t*x1*x2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*t*x1*x3*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*t*x2**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + 2*t*x2*x3*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + 2*t*y1*y2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*t*y1*y3*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*t*y2**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + 2*t*y2*y3*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + x1**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*x1*x2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + x2**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + y1**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) - 2*y1*y2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + y2**2*sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2) + sqrt(x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2)*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2)*sqrt(t**2*x2**2 - 2*t**2*x2*x3 + t**2*x3**2 + t**2*y2**2 - 2*t**2*y2*y3 + t**2*y3**2 - 2*t*x2**2 + 4*t*x2*x3 - 2*t*x3**2 - 2*t*y2**2 + 4*t*y2*y3 - 2*t*y3**2 + x2**2 - 2*x2*x3 + x3**2 + y2**2 - 2*y2*y3 + y3**2)
Is Stewart Theorem true? False
와우! 위 결과의 각각의 식들을 봐봐. 엄청 길고 복잡해서 육안으로 비교는 불가능하네. 그래서 doit()이라는 계산함수, expand()라는 전개함수들을 써서 식들을 최대한 같은 방향으로 계산해 놓고 equal 여부를 판단해 봤지. 그랬더니 답이
False
이네.
그럼 스튜어트 정리는 틀린 걸까? sympy의 항등식 판단은 좀 엄밀해서, 같은 식인데도 불구하고 표현이나 전개 및 정리 여부에 따라 같은 식을 다른 식이라 간주할 수 있는 단점이 있어.
아무래도 결과식 자체가 너무 복잡해서 sympy가 이를 분석하기에는 놓치는 부분이 많을 거 같은 생각이야,
그럼 약간 짱구를 굴려, 결과를 육안으로 비교 가능하게끔 간단히 나오도록 해볼 수 있을까?
python code (아름다운 방법)
위 코드는 $x_i , y_i$들에 점 $X$를 나타내는 매개변수 $t$ 까지 많은 변수들이 얽히고설켜 결과 자체가 복잡하게 나왔다는 게 문제! 따라서 위의 삼각형을 이리저리 평행이동 및 회전애 보면서, 다음과 같이 좌표계를 도입해 보자고.
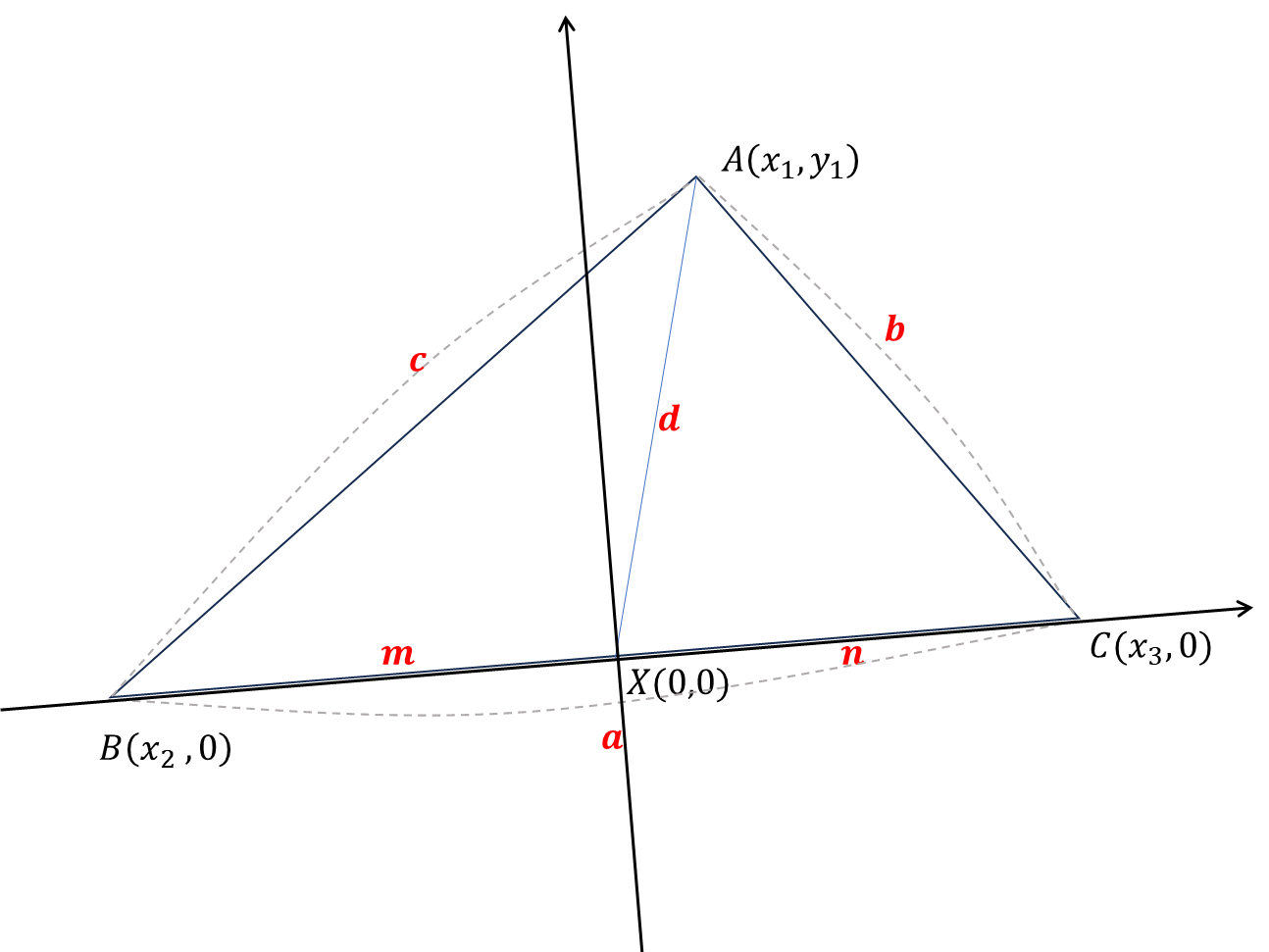
$X$라는 점을 표현하는데 많은 공수가 들어갔으니, 이 친구를 아예 원점으로 박아버리는 거야. 그리고 선분 $BC$가 $x$축에 올라오게끔 두는 거지. 그러면
$$A(x_1, y_1)~,~ B(x_2, 0)~,~ C(x_3, 0) $$
라 표현가능하고, 무엇보다 $X$가 원점이지! 그리고 $X$가 $BC$를 갈라야 하므로
$$ x_2 <0~,~ x_3 >0 \tag {2}$$
라는 조건이 숨어 있어.
그러면, 이런 상황에서 python code를 짜볼게.
from sympy import *
x1, y1= symbols("x1 y1")
x2 = symbols("x2")
x3= symbols("x3")
A = Point(x1, y1)
B = Point(x2, 0)
C = Point(x3, 0)
X = Point(0,0)
a = B.distance(C)
b = A.distance(C)
c = A.distance(B)
d = A.distance(X)
m = B.distance(X)
n = C.distance(X)
eqn1 = b ** 2 * m + c ** 2 * n
eqn1 = expand(eqn1)
eqn2 = a * (d ** 2 + m * n)
eqn2 =expand(eqn2)
print('LHS of Stewart Theorem')
print(eqn1)
print('RHS of Stewart Theorem')
print(eqn2)
print(f'Is Stewart Theorem true? {eqn1 == eqn2}')
앞선 코드와 비슷하므로 설명은 생략. 결과를 얼른 볼까?
LHS of Stewart Theorem
x1**2*sqrt(x2**2) + x1**2*sqrt(x3**2) - 2*x1*x2*sqrt(x3**2) - 2*x1*x3*sqrt(x2**2) + x2**2*sqrt(x3**2) + x3**2*sqrt(x2**2) + y1**2*sqrt(x2**2) + y1**2*sqrt(x3**2)
RHS of Stewart Theorem
x1**2*sqrt(x2**2 - 2*x2*x3 + x3**2) + y1**2*sqrt(x2**2 - 2*x2*x3 + x3**2) + sqrt(x2**2 - 2*x2*x3 + x3**2)*sqrt(x2**2)*sqrt(x3**2)
Is Stewart Theorem true? False
뭐꼬? 아직도 식들이 복잡하게 나와. 그리고 심지어 스튜어트 정리가 틀렸다고 결론을 냈네.
그런데 한 가지 사실, 식(2)을 적용하질 않았어. 게다가 위의 결과를 자세히 들여다보면
sqrt(x2**2) , sqrt(x3**2)
처럼 제곱하였다가 루트를 씌웠는데, 정리를 더 안 하고 가만히 놔두는 식들이 보이네?
이러한 현상이 발생하는 이유는, sympy는 아주 엄밀해서 루트를 그냥 벗겨주지 않아. 일례로, 어떤 실수 $a$에 대해
$$ \sqrt{a^2 } = a $$
라고 풀어주지 않아. 왜냐면, $a$가 symbol이지만 음수일 수도 있잖아? 괜히 이렇게 루트를 벗겨서 계산을 진행해 나가다가는 결과가 아주 엉망이 될 수도 있는 거지. 그래서 우리는 식(2)의 부호를 symbol임을 선언할 때, 정의해 주려고 해
위 코드에서
x2 = symbols("x2")
x3 = symbols("x3")
이 부분 보이지? 이 부분을 조금 더 엄밀하게
x2 = symbols("x2", negative=True)
x3 = symbols("x3", positive=True)
이렇게 바꿔볼 거야. 그러면 결과는
LHS of Stewart Theorem
-x1**2*x2 + x1**2*x3 + x2**2*x3 - x2*x3**2 - x2*y1**2 + x3*y1**2
RHS of Stewart Theorem
-x1**2*x2 + x1**2*x3 + x2**2*x3 - x2*x3**2 - x2*y1**2 + x3*y1**2
Is Stewart Theorem true? True
식이 엄청 간결해졌지? 눈으로 비교도 가능할 정도야. 당연히 스튜어트 정리가 참이라는 결론을 내주고 있네.
정리
일단 잊지 말아야 할 것은
$$ \sqrt{a^2} = |a| $$
라는 것. 그리고 이것을 sympy로 대충 풀려했다가는 $\sqrt{a^2}$은 그냥 sqrt(a**2)로 남게 된다는 것!!
이 글에서 쓰인 함수들을 정리해 보자면,
| symbols("x", negative = True) | 음수인 변수기호 x 정의 |
| symbols("x", positve = True) | 양수인 변수기호 x 정의 |
| expand() | 식의 전개 |
'파이썬으로 풀어보는 고딩수학 > 평면좌표' 카테고리의 다른 글
| 수직으로 만나는 점, 직선 구하기 (0) | 2023.12.18 |
|---|---|
| 육각형 속 마름모(@puzzlist의 기하문제) (0) | 2023.12.15 |
| 파푸스의 중선 정리 with Sympy (0) | 2023.12.13 |
| 삼각형의 무게중심을 sympy로 구하기 (0) | 2023.12.06 |
| 직각삼각형 만들기 (0) | 2023.12.01 |




댓글