이번 글에서는 여러 개의 자산(주식, 채권, 파생상품 등)을 분산투자여 포트폴리오를 만들었을 때, 그 포트폴리오가 주는 위험과 기대수익률의 관계에 대해서 고찰해 볼까 합니다.
먼저 소개할 것은 아주 오래된 이론이지만 지금도 강력하게 쓰이는
평균 - 분산 포트폴리오 이론
입니다. 왜 평균과 분산이 갑툭튀인 걸까요? 내용은 간단한 가정에서 출발합니다.
어느 투자자산 A가 있고 그 투자자산의 수익률 데이터를 생각해 봅시다.
○ 투자자산에서 기대할 수 있는 수익률은 A의 수익률 데이터의 기댓값, 즉 평균입니다.
○ 반면 이 투자자산 A에 투자했을 때의 위험은 바로 표준편차(또는 분산)가 될 것입니다. 분산이 작은 경우에는 A의 수익률 데이터가 평균 근처에 몰려 있다는 뜻이므로, 안정적인 기대수익률을 예상해 볼 수 있겠죠. 하지만 분산이 큰 경우에는 수익률 분포가 평균에서 멀리 떨어져 분포하게 되므로 수익률이 엄청 크게 나올 수도, 반대로 수익률이 처참할 수도 있는 것이겠죠. 즉 투자의 리스크가 있다는 이야기입니다.
이런 개념을 이용하여,
어떠 자산에 투자할 때 투자리스크는 수익률의 분산(또는 표준편차)
로 생각하는 경우가 많습니다.
자산에 투자할 때, 투자자들은 가장 위험하지 않은 자산에 투자하여 가장 높은 수익률을 올리고 싶어 합니다. 하지만 이건 꿈같은 이야기겠죠. 높은 수익률을 얻기 위해서는 다소 모험을 즐겨야 합니다. 리스크를 어느 정도 감내할 수 있는 그릇이 되어야 큰 수익을 담을 수 있겠죠. 이른바
High Risk, High Return
입니다.

얼마나 유명한 말인지 노래로도 있습니다.

그런데 높은 수익을 얻기 위해 위험을 엄청나게 짊어지는 투자자는 없겠죠. 투자자들은 다양한 투자 자산을 비교해 봅니다. 비교를 통해
○ 같은 위험(분산)을 가지지만, 기대 수익률이 더 좋은 자산
○ 같은 기대수익률 중에서 위험(분산)이 가장 낮은 자산
을 선택하게 됩니다. 시장에 주어진, 내가 투자할 수 있는 자산이 많으면 좋겠지만, 한계가 있을 수 있죠. 그래서 투자자들은 주어진 자산들을 적절히 섞어 분산투자를 생각해 봅니다. 내가 가진 돈으로 이것저것 섞어서 투자를 해 보죠. 이러한 과정을 "포트폴리오를 만든다"라고 합니다.
요지는 이렇습니다.
① 시장에 주어진 자산을 이리저리 섞어 봅니다 (포트폴리오 만들기)
② 그 포트폴리오를 만드는 방법에 따라 기대수익률과 위험(분산)을 구해 봅니다.
③ 기대수익률과 위험의 관계를 파악하여 내 마음에 쏙 드는 포트폴리오를 선택!!
간단한 경우, 시장에 투자 자산이 두 개인 경우부터 알아봅시다.
두 개 자산의 기대수익률과 리스크
두 자산 $X_1, X_2$ 의 기대수익률을 $r_1,r_2$, 수익률의 표준편차를 $\sigma_1 , \sigma_2$라 합시다.
만일 이 두 자산을 적절히 섞어서 투자한다고 합시다. 이른바 포트폴리오를 만드는 거죠.
두 자산이 각각 가중치 $w_1, w_2$를 가지고 편의상
$$ w_1+w_2 =1$$
이라 합시다. 또 두 자산 모두 매수한 상황이라고 가정합니다. 즉
$$ w_1 , w_2 \geq 0$$
이죠.
이때, 포트폴리오
$$ X= w_1 X_1 +w_2 X_2$$
의 기대수익률과 표준편차를 각각 구해봅시다.
포트폴리오의 기대수익률
기대수익률은 쉽습니다.
$$
\begin{align}
\mathbb{E}(X) & = \mathbb{E}(w_1X_1+w_2 X_2) \\
& = w_1 \mathbb{E}(X_1) +w_2 \mathbb{E}(X_2)\\
& = w_1 r_1 + w_2r_2
\end{align}
$$
입니다.
포트폴리오의 분산
$X$의 표준편차를 구하기 전, 분산을 먼저 구해보죠.
$$
\begin{align}
\mathbb{V}(X) &= \mathbb{E}(X^2) -(\mathbb{E}(X))^2\\
& = \mathbb{E}( (w_1X_1+w_2X_2)^2)- (w_1 \mathbb{E}(X_1)+w_2 \mathbb{E}(X_2))^2\\
& = w_1^2 \mathbb{E}(X_1^2) + 2w_1w_2 \mathbb{E}(X_1X_2)+w_2^2\mathbb{E}(X_2^2)\\
& ~~~~~~~~~~~~-\left(w_1^2 \mathbb{E}(X_1)^2 +2w_1w_2 \mathbb{E}(X_1)\mathbb{E}(X_2) +w_2^2 \mathbb{E}(X_2)^2\right)\\
& = w_1^2 (\mathbb{E}(X_1^2)-\mathbb{E}(X_1)^2 ) + w_2^2(\mathbb{E}(X_2^2)-\mathbb{E}(X_2)^2) +2w_1w_2(\mathbb{E}(X_1X_2)-\mathbb{E}(X_1)\mathbb{E}(X_2))\\
& = w_1^2 \mathbb{V}(X_1) +w_2^2 \mathbb{V}(X_2) +2w_1 w_2 \mathbb{Cov}(X_1,X_2)\\
& = w_1^2 \sigma_1^2 +w_2^2 \sigma_2^2 + 2w_1w_2 \rho \sigma_1\sigma_2 \tag{1}
\end{align}
$$
공분산 $\mathbb{Cov}(\cdot,\cdot)$ 은 여기를 참고하시기 바랍니다. 위 식에서 $\rho$는 두 자산 $X_1, X_2$의 상관계수(correlation)를 뜻하고
$$ \rho = \mathbb{Corr}(X_1,X_2) = \frac{\mathbb{Cov}(X_1,X_2)}{\sigma_1\sigma_2}$$
입니다.
식(1)은 아래와 같이 좀 더 멋지게 쓸 수 있습니다.
$$
\mathbf{w} = \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} ~,~ \mathbf{C} =\begin{pmatrix} \sigma_1^2 & \rho\sigma_1\sigma_2 \\ \rho\sigma_1\sigma_2 & \sigma_2^2 \end{pmatrix}$$
라 합시다. 즉 $\mathbf{C}$는 공분산 행렬입니다.
그러면 식 (1)은
$$ \mathbf{V}(X) = \mathbf{w}^t \mathbf{C} \mathbf{w}$$
처럼 행렬의 곱셈으로 간단히 쓸 수 있습니다.
여러 자산의 기대수익률과 리스크
위의 관찰을 확정하여, 만일 투자자산이 $n$개인 경우는 어떨까요? 자산을 $X_1 ,X_2, \cdots, X_n$이라 하고,
각 $1\leq i\leq n$에 대해, $X_i$의 기대수익률을 $r_i$, 표준편차를 $\sigma_i$라 합시다.
각각의 자산 $X_i$ 에 가중치 $w_i$ 씩을 주고, 위의 2 자산 경우처럼
$$w_1+w_2+\cdots + w_n =1~~,~~ w_i \geq 0 $$
이라 가정합시다.
이제, 포트폴리오
$$ X = \sum_{i=1}^n w_i X_i = w_1X_1+\cdots +w_n X_n$$의 기대수익률과 분산을 구해보도록 하죠.
포트폴리오의 기대수익률
기대수익률은 아래와 같습니다.
$$ \mathbb{E}(X) = \sum_{i=1}^n w_i \mathbb{E}(X_i ) = \sum_{i=1}^n w_i r_i$$입니다.
포트폴리오의 분산
분산은 조금 복잡해지는데요. 먼저 다음의 두 식을 구하죠.
$$ \mathbb{E}\left( \left( \sum_{i=1}^n w_i X_i \right)^2 \right) =\sum_{i=1}^n w_i^2 \mathbb{E}(X_i^2) + 2\sum_{1\leq i<j\leq n} w_iw_j \mathbb{E}(X_iX_j) $$ 이고
$$
\begin{align}
\mathbb{E} \left( \sum_{i=1}^n w_i X_i \right)^2 &= \left( \sum_{i=1}^n w_i \mathbb{E}(X_i) \right)^2 \\
& = \sum_{i=1}^n w_i^2 \mathbb{E}(X_i)^2 +2\sum_{1\leq i<j\leq n} w_iw_j \mathbb{E}(X_i)\mathbb{E}(X_j)\\
\end{align}
$$
입니다. 따라서
$$
\begin{align}
\mathbb{V}(X) &= \mathbb{E}(X^2) -\mathbb{E}(X)^2\\
& = \sum_{i=1}^n w_i^2( \mathbb{E}(X_i^2)-\mathbb{E}(X_i)^2) +2\sum_{1\leq i<j\leq n} w_iw_j \left( \mathbb{E}(X_iX_j) - \mathbb{E}(X_i)\mathbb{E}(X_j)\right) \\
& = \sum_{i=1}^n w_i^2 \sigma_i^2 + 2\sum_{1\leq i<j\leq n} w_iw_j \rho_{ij} \sigma_i\sigma_j \tag{2}
\end{align}
$$
입니다. 위 식에서 $\rho_{ij}$는 자산 $X_i , X_j$사이의 상관계수이고 수식으로는
$$ \rho_{ij} = \frac{\mathbb{Cov}(X_i,X_j)}{\sigma_i \sigma_j} $$
입니다.
식(2)도 행렬의 곱의 형태로 멋지게 쓸 수 있습니다.
$$
\mathbf{w} = \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\w_n \end{pmatrix} ~,~
\mathbf{C} =\begin{pmatrix}
\sigma_1^2 & \rho_{12}\sigma_1\sigma_2 & \cdots & \rho_{1n} \sigma_1\sigma_n\\
\rho_{12}\sigma_1\sigma_2 & \sigma_2^2 & \cdots & \rho_{2n} \sigma_2\sigma_n \\
\vdots & \vdots & \ddots & \vdots \\
\rho_{n1}\sigma_1\sigma_n & \rho_{n2}\sigma_2\sigma_n & \cdots & sigma_n^2
\end{pmatrix},$$
즉 $\mathbf{w}$는 가중치 벡터, $\mathbf{C}$는 공분산 행렬이라 하면, 자산 2개 있을 때와 마찬가지로 수식(2)을
$$ \mathbf{V}(X) = \mathbf{w}^t \mathbf{C} \mathbf{w}\tag{3}$$
와 같이 쓸 수 있습니다.
Python Code
두 자산을 섞은 포트폴리오 구현
상관계수 $\rho$를 갖는 두 자산 $X_1, X_2$를 잘 섞어 다양한 포트폴리오를 구현해 보겠습니다.
임의의 양수 가중치 $w_1,w_2 \geq 0$을 두어($w_1+w_2=1$ 가정) 다양한 포트폴리오를 만든 뒤, 이 포트폴리오의 표준편차와 기대수익률을 $x$축이 표준편차, $y$축이 기대수익률이 되도록 scattering 해 보죠.
def TwoAsset_Portfolio():
rate = np.array([0.02, 0.03]) # 두 자산의 수익률: 2%, 3%
std = np.array([0.05, 0.12]) # 두 자산의 수익률표준편차: 5%, 12%
weight = np.linspace(0, 1, 100 + 1) # 첫번째 기초자산 가중치 : 0~1 100등분
corr = np.linspace(-1, 1, 10 + 1) # 두 자산의 상관계수를 -1~1 까지 10등분
colors = cm.Blues(np.linspace(0.1, 1, len(corr))) # 각 correlation마다 Blue계열의 색을 쓰기 위한 color map도입
legend_showed = [0, len(corr) - 1] # 범례 표시는 corr[0]과 corr[-1] 두 경우만 하기 위해
for i, (rho, cc) in enumerate(zip(corr, colors)):
if i in legend_showed: # 범례 표시
mylabel = 'corr={:.1f}'.format(rho)
else:
mylabel = None # 범례표시 안함 None
rate_port = []
std_port = []
for w in weight:
w1 = w # 자산1 가중치
w2 = 1 - w # 자산2 가중치 : w1 + w2=1 이 되게끔
rate_port.append(w1 * rate[0] + w2 * rate[1])
# portfolio의 기대수익률
std_port.append(np.sqrt(w1 ** 2 * std[0] ** 2 + w2 ** 2 * std[1] ** 2 + 2 * rho * w1 * w2 * std[0] * std[1]))
# portfolio의 표준편차
plt.scatter(std_port, rate_port, color=cc, label=mylabel)
# (표준편차, 기대수익률) 을 xy평면에 scattering
plt.legend()
plt.xlabel('std')
plt.ylabel('expectation')
plt.show()
결과 그림을 보시죠.
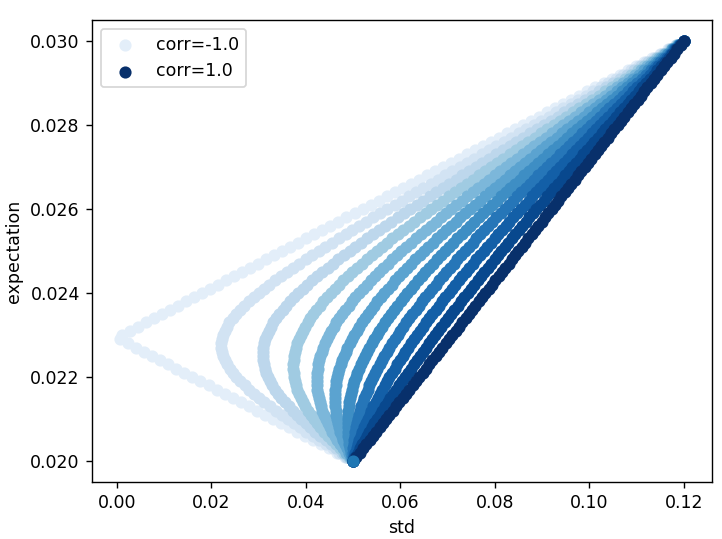
상관계수가 -1일 때가 제일 왼쪽의 그래프입니다. 완전한 꺾은 선이네요.
상관계수가 1일 때는 두 점을 잇는 직선이 됩니다. 두 점이란 바로 $(\sigma_1,r_1) $과 $(\sigma_2, r_2)$ 겠죠.
상관계수가 -1에서 1 사이는 왼쪽으로 볼록한 곡선이 됩니다. 표준편차가 커지면(즉 위험이 증가하면) 기대수익률도 커지는 현상도 보이고요. 또한 표준편차를 최소로 하면서 기대수익률을 어느 정도 바라볼 수 있는
최소분산 포트폴리오
를 찾을 수도 있습니다.
예컨대, $\rho=0.2$ 인 상황을 봅시다. 최소분산이 어디에서 일어나는지 찾아보기 위해 위의 코드와 아주 비슷한 코드를 하나 새로 작성해 봅시다.
def TwoAsset_Portfolio_fixedCorrelation():
rate = np.array([0.02, 0.03])
std = np.array([0.05, 0.12])
weight = np.linspace(0, 1, 100 + 1)
corr = 0.2
rate_port = []
std_port = []
for w in weight:
w1 = w
w2 = 1 - w
rate_port.append(w1 * rate[0] + w2 * rate[1])
std_port.append(np.sqrt(w1 ** 2 * std[0] ** 2 + w2 ** 2 * std[1] ** 2 + 2 * corr * w1 * w2 * std[0] * std[1]))
rate_port = np.array(rate_port)
std_port = np.array(std_port)
plt.scatter(std_port, rate_port, color='skyblue', s=20) # 우선 (표준편차, 기대수익률) scattering
std_min_x = std_port[std_port == np.min(std_port)] # 표준편차를 최소로 하는 index 에 해당하는 표준편차 값
std_min_y = rate_port[std_port == np.min(std_port)] # 표준편차를 최소로 하는 index 에 해당하는 기대수익률 값
plt.scatter(std_min_x, std_min_y, color='blue', s=50) # plot dot
print('w1={:.2f}'.format(weight[std_port == np.min(std_port)][0])) # 표준편차를 최소로 하는 index에 해당하는 w1 가중치
plt.xlabel('std')
plt.ylabel('expectation')
plt.show()
결과는 다음과 같습니다.
w1=0.91즉, $w_1=0.91 , w_2=0.09$일 때 분산이 최소가 나온다라는 것이죠. 자산 $X_1$에 91%를 투자하고 $X_2$에는 9% 투자할 때 분산이 최소가 된다는 뜻입니다. 바로 최소분산 포트폴리오이죠. 그래프는 아래와 같습니다.
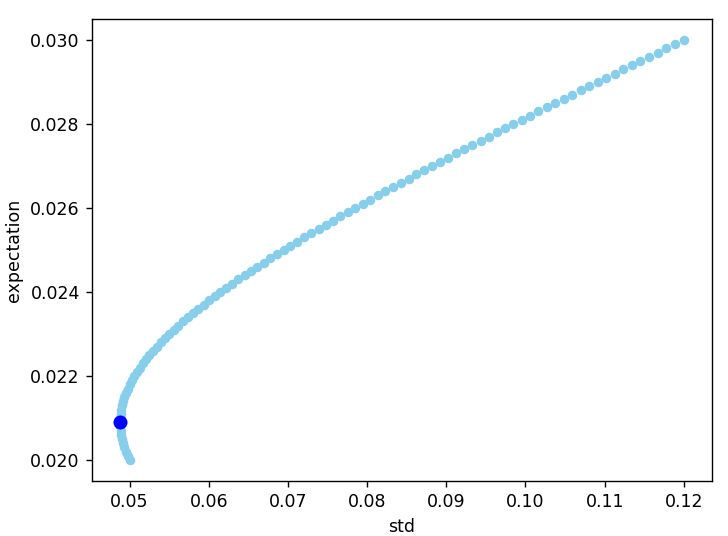
사실 위 점은 수식을 통해서도 찾아낼 수 있습니다. 포트폴리오 $X$의 분산은
$$ \mathbb{V}(X) = w_1^2 \sigma_1^2 + w_2^2\sigma_2^2 + 2\rho w_1 w_2 \sigma_1\sigma_2$$
라 했습니다. $w_1 = w$ 라 하면 $w_2 =1-w$이므로 위 분산식을 $f(w)$ 라 하면
$$ f(w) = \sigma_1 w^2 + \sigma_2(1-w)^2 + 2\rho \sigma_1\sigma_2 w(1-w)$$
입니다.
따라서
$$ f'(w) = (\sigma_1^2+\sigma_2^2 -2\rho \sigma_1\sigma_2)w +(\rho \sigma_1\sigma_2-\sigma_2^2) $$
이고
$$ f''(w) = \sigma_1^2 +\sigma_2^2 -2\rho\sigma_1\sigma_2$$입니다.
$f''(w) = (\sigma_1-\sigma_2)^2 + 2(1-\rho)\sigma_1\sigma_2 > 0$이므로 아래로 볼록 합니다. 따라서 $f'(w)=0$ 점이 바로 최솟값이 되겠죠, 즉,
$$ w= \frac{-\rho \sigma_1\sigma_2+\sigma_2^2}{\sigma_1^2+\sigma_2^2 -2\rho\sigma_1\sigma_2} \tag{4}$$
일 때이죠.
만일 $\rho \leq \sigma_2/\sigma_1 ~,~ \rho \leq \sigma_1/\sigma_2$ 까지 만족한다면,
식(4)의 $w$는
$$ 0\leq w \leq 1$$
까지 만족합니다. 바로 우리가 찾는 식이죠. 아래와 같이 검산해 볼 수 있습니다.
rate = np.array([0.02, 0.03])
std = np.array([0.05, 0.12])
corr = 0.2
if (corr <= std[0] / std[1]) and (corr <= std[1] / std[0]):
print('Condition True')
w = (std[1] ** 2 - corr * std[0] * std[1]) / (std[0] ** 2 + std[1] ** 2 - 2 * corr * std[0] * std[1])
print('w1={:.4f}'.format(w))
-------------------------------------------------------
Condition True
w1=0.9103
세 자산을 섞은 포트폴리오 구현
이번에는 세 개의 자산으로 분석합니다. 식(3)을 이용하여 포트폴리오의 분산을 구할 예정입니다.
마찬가지로 세 포트폴리오의 가중치 합이 1이 되게 하여, 포트폴리오의 기대수익률과 분산을 구합니다.
위의 예제랑 좀 다른 점은 가중치 합이 1이 되는 세 가중치를 이번에는 난수를 발생시켜 합이 1이 되게 조정해 주는 방법을 택했습니다.
def ThreeAsset_Potfolio():
rate = np.array([0.02, 0.03, 0.04])
std = np.array([0.01, 0.12, 0.2])
rho12 = 0.1
rho13 = 0.2
rho23 = -0.1
s12 = std[0] * std[1] * rho12 # 공분산행렬의 (1,2)원소
s13 = std[0] * std[2] * rho13 # 공분산행렬의 (1,3)원소
s23 = std[1] * std[2] * rho23 # 공분산행렬의 (2,3)원소
cov_matrix = np.array([[std[0] ** 2, s12, s13],
[s12, std[1] ** 2, s23],
[s13, s23, std[2] ** 2]]) # 공분산 행렬
rate_port = []
std_port = []
for i in range(500):
w = np.random.rand(3) # 균등난수 3개 w1,w2,w2를 발생하여
w /= w.sum() # 그 합인 W= w1+w2+w3으로 나누면 w1/W , w2/W, w3/W 의 합은 1
rate_result = w @ rate.T # 기대 수익률은 w1r1 + w2r2 + w3r3 이므로 w와 r의 행렬곱
std_result = np.sqrt(w @ cov_matrix @ w.T) # 분산값 wCw'
rate_port.append(rate_result)
std_port.append(std_result)
rate_port = np.array(rate_port)
std_port = np.array(std_port)
plt.style.use('seaborn') # plot style 지정
colors = rate_port / std_port
plt.scatter(std_port, rate_port, c=colors, cmap=cm.autumn) #autumn color map으로 scattering
plt.xlabel('std')
plt.ylabel('expectation')
plt.show()
결과는 아래와 같습니다. 투자자산이 2개일 때와 비슷하게 약간 볼록성이 느껴지는 관계 그래프가 나오네요.
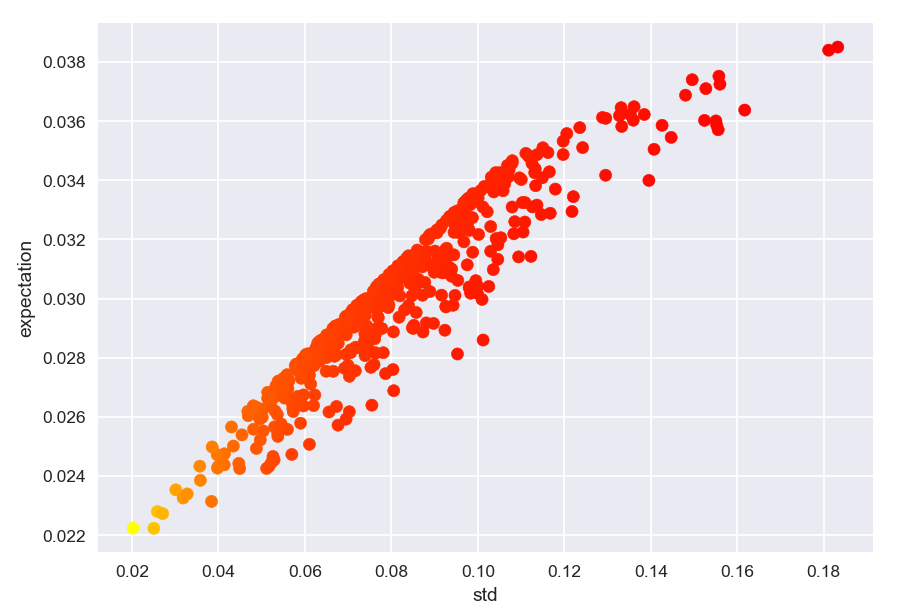
댓글