이번 글에서는
2022.08.25 - [금융공학] - 배리어옵션 -UOC 옵션 #2 함축적 FDM
배리어옵션 -UOC 옵션 #2 함축적 FDM
이번 글은 지난 글 2022.08.24 - [금융공학] - 배리어옵션 -UOC 옵션 #1 수학공식(Closed form) 배리어옵션 -UOC 옵션 #1 수학공식(Closed form) 저번 글까지 파생상품의 대표주자 옵션의 프리미엄을 다양한 방
sine-qua-none.tistory.com
에서 다뤘던 내용중 미처 자세하게 살펴보지 못한 사항에 대해 다룰 예정입니다.
UOC 옵션의 가격을 계산하기 위해 지금까지
○ Closed Form 을 사용 : 2022.08.24 - [금융공학] - 배리어옵션 -UOC 옵션 #1 수학공식(Closed form)
○ FDM(함축적 방법) 사용: 2022.08.25 - [금융공학] - 배리어옵션 -UOC 옵션 #2 함축적 FDM
의 두 가지 방법으로 접근해 봤습니다. 하지만,
두 방식의 결과가 조금 다르다?
저번 글에서 다루었던 결과를 먼저 볼까요?

파란 곡선은 FDM 으로 구한 UOC의 가격, 붉은 곡선은 Closed Form으로 구한 UOC의 가격입니다.
왜 차이가 날까요? 결정적인 원인이 있었습니다. 바로
Closed Form으로 구한 가격은 기초자산 주가의 연속적인 움직임을 반영한 결과인 반면, FDM은 이산적인(discrete) 격자에서의 이산적인 움직임을 반영한 결과
이기 때문입니다. 구체적으로 설명하기 위해 다음의 그림을 보겠습니다.

위 그래프를 만든 조악한 코드
def Make_chart():
stock = [115,
115.5191387,
120.9573279,
119.6829095,
122.7819065,
121.1889859,
124.3598548,
120.2820719,
118.7612287,
117.1747377,
115.7504649,
116.3815683,
110.4325561,
111.0230136]
barrier = 120
plt.plot(stock, color ='gray')
plt.plot(0, stock[0], marker='o',markersize= 10, color ='k')
plt.plot(len(stock)-1,stock[-1], marker='o', markersize= 10, color='k')
plt.hlines(barrier, 0, len(stock)-1, color='r')
plt.vlines(0, 110, stock[0], linestyles ='--', color='grey')
plt.vlines(len(stock)-1, 110, stock[-1], linestyles='--', color='grey')
plt.text(0.2 ,110, '$S_j$', fontsize =20)
plt.text(len(stock)-1+0.2, 110, '$S_{j+1}$', fontsize=20)
plt.gca().axes.xaxis.set_visible(False)
plt.show()
$S_j$와 $S_{j+1}$ 은 FDM 격자에서 연이어진 주가라고 합시다. 하지만 GBM 모델은 연속이므로 $S_j$와 $S_{j+1}$사이에도 빽빽한 움직임을 보여주겠죠. 위의 그림을 보시면
○ FDM으로 푸는 경우: 배리어를 치지 않은 상황입니다. 연이어진 주가 모두 배리어 밑에 있으니까요
○ GBM의 연속성을 바탕으로 푼 Closed Form : 배리어를 친 상황이 됩니다.
따라서 이산화를 시킴으로써 현격하게 차이가 발생합니다. 예전 글에서 다루었던 콜옵션 같은 경우는 어차피 만기 때의 기초자산 가격이 중요하므로 이런 일은 벌어지지 않죠.
아무리 FDM 기초자산 축의 간격을 좁게 해도, 연속성을 기반으로 푼 Closed Form 과는 차이가 나는 겁니다.
그러면, 연속을 기반으로 한 풀이를 어떻게 하면 이산적인 풀이와 근사 시킬 수 있을까요?
배리어 조정
연속성과 이산성 각각으로 구한 해를 서로 근사시키는 방법으로 배리어의 높낮이를 조정하는 하는 방법이 있습니다. 다음은 ON PRICING OF DISCRETE BARRIER OPTIONS라는 논문(S. G. Kou, Columbia University)에서 찾은 이론인데요, 소개를 해보겠습니다.
배리어 조정
배리어가 $H$인 UOC의 연속성을 기반으로 한 가격을 $V(H)$라 하고, $m$번 관찰 기회가 주어진 배리어 $H$의 UOC 가격을 $V_m(H)$라 합시다. 그러면
$$ V_m(H) = V(He^{\beta \sigma \sqrt{T/m}})+\omicron(1/\sqrt{m})\tag{*}$$
이 성립합니다. 여기서 $\beta \approx 0.5826$ 정도 되는 수입니다.
위 식의 뜻이 뭘까요? small o 기호의 정의에 따르면,
$$ \lim_{m\rightarrow \infty} \frac{V_m(H)- V(H e^{\beta \sigma \sqrt{T/m}})}{1/\sqrt{m}} =0$$
이라는 얘기입니다. 즉 분자인 $V_m$과 $V$의 차이가 $m^{-1/2}$보다 더 빨리 수렴하다는 이야기겠죠. $m$이 커질수록 $m^{-1/2}$는 0으로 다가가므로 $V_m$과 $V$의 값이 가까워진다는 뜻입니다.
$V_m$은 이산적인 가격이므로 FDM의 주가 grid를 $m$개로 쪼개서 구한 결과라 생각할 수 있습니다. 반면 $V$는 연속적이므로 Closed Form이라 간주할 수 있죠. 따라서 결론은
UOC의 Closed Form에 배리어를 조금 상향해서 넣으면 FDM 결과에 더욱 근사한다,
상향하는 정도는 $e^{\beta \sigma \sqrt{T/m}}$이다.
라는 뜻이 됩니다. 정말인지 한번 볼까요?
Python Code
지난 글 2022.08.25 - [금융공학] - 배리어옵션 -UOC 옵션 #2 함축적 FDM
에 수록된 code 중 calculate_UOC 함수를 살짝 수정했습니다.
def calculate_UOC():
s0 = 100
strike = 100
maturity = 1
upBarrier = 120
rfr = 0.02
vol = 0.2
div = 0.01
rebate = 3
sSeries = np.linspace(s0 / 2, upBarrier, 101)
uoc_value_fdm, sGrid, tGrid = UOC_price_FDM_implicit(s0, strike, maturity, upBarrier, rfr, vol, div, rebate)
result_FDM = np.interp(sSeries, sGrid, uoc_value_fdm[-1, :])
result_closed_form = np.array(
[UOcall_ClosedForm(spot, strike, maturity, upBarrier, rfr, vol, div, rebate) for spot in sSeries])
# 배리어를 조정함
upBarrier = upBarrier * np.exp(0.5826 * vol * np.sqrt(maturity / 250))
result_closed_form_adjusted = np.array(
[UOcall_ClosedForm(spot, strike, maturity, upBarrier, rfr, vol, div, rebate) for spot in sSeries])
print('UOC_value_FDM: {}'.format(np.interp(s0, sGrid, uoc_value_fdm[-1, :])))
# 조정된 배리어로 closed form을 구함
print('UOC_value_ClosedForm_Adjusted: {}'.format(UOcall_ClosedForm(s0, strike, maturity, upBarrier, rfr, vol, div, rebate)))
# FDM 결과를 그래프로 표시
plt.plot(sSeries, result_FDM, label='FDM value')
# 배리어 조정전 Closed form 결과
plt.plot(sSeries, result_closed_form, label='Closed Form Value')
# 배리어 조정후 Closed form 결과
plt.plot(sSeries, result_closed_form_adjusted, label='Closed Form Value(Barrier Adjusted)')
plt.legend()
plt.show()지난 글의 설명을 참고하면 되고, 가장 중요한 부분은
# 배리어를 조정함
upBarrier = upBarrier * np.exp(0.5826 * vol * np.sqrt(maturity / 250))이렇게 조정한 부분입니다. FDM의 시간축을 250등분 했기 때문에 관찰 횟수 $m$을 250회로 보고 조정한 결과입니다.
결과를 볼까요?
UOC_value_FDM: 2.223138681295252
UOC_value_ClosedForm_Adjusted: 2.226719407812769아름답네요. FDM과 Closed form 결과의 간극이 배리어 조정을 통해 극복이 됩니다. 그래프를 그려보면 아래와 같습니다.
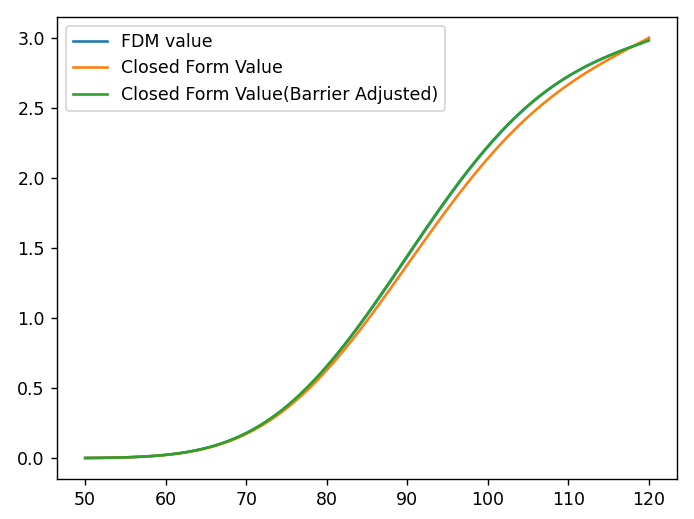
FDM을 뜻하는 파란 곡선과 배리어 조정을 가미한 Closed form 결과가 거의 유사합니다.
위의 결과는 연속성 기반의 closed form을 이산적 형태의 결과로 바꾼 거죠? 그럼 거꾸로 이산적 형태의 결과를 연속적 해로 바꾸기 위해서는 어찌하면 될까요?
$$ V_m(H) = V(He^{\beta \sigma \sqrt{T/m}})+\omicron(1/\sqrt{m})$$ 이었으므로
$$ V(H)\approx V_m(He^{-\beta \sigma \sqrt{T/m}})$$
가 성립할 것입니다. 즉 FDM 함수에 배리어 조정 팩터$e^{-\beta \sigma \sqrt{T/m}}$를 곱한 배리어를 input으로 하여 얻은 결과는 closed form $V$에 원래 배리어를 input으로 대입하여 얻은 결과와 똑같습니다. 즉
# 이산배리어를 연속배리어로 조정하는 과정
upBarrier_adjust = upBarrier * np.exp(-0.5826 * vol * np.sqrt(maturity / 250))
# 조정된 배리어를 FDM에 대입하면 closed form 결과로 근사됨
uoc_value_fdm, sGrid, tGrid = UOC_price_FDM_implicit(s0, strike, maturity, upBarrier_adjust, rfr, vol, div, rebate)
# 원래 배리어에 대한 closed form
result_closed_form = np.array(
[UOcall_ClosedForm(spot, strike, maturity, upBarrier, rfr, vol, div, rebate) for spot in sSeries])
를 하여 결과를 보면,
UOC_value_FDM: 2.1671086725957083
UOC_value_ClosedForm: 2.1397093466460846가 나옵니다. 두 값이 근사하게 근사하죠. 그래프를 그려보면
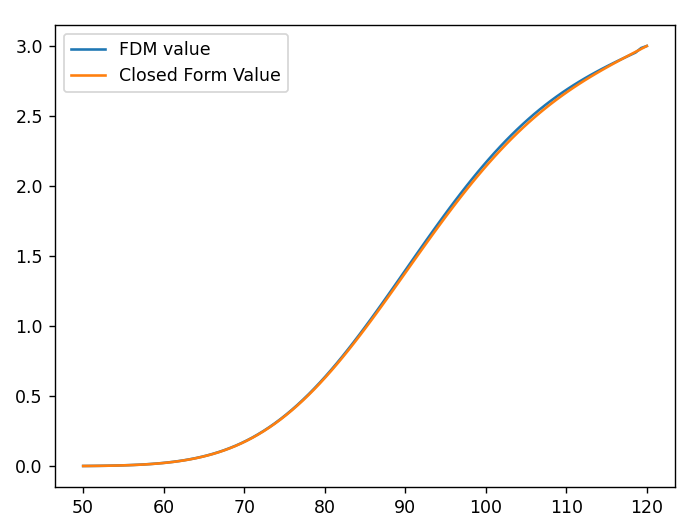
역시 근사합니다. 배리어 조정을 통해 연속적인 해와 이산적인 해를 왔다 갔다 할 수 있는 것입니다.
여담
식 (*)의 $\beta$는 사실
$$ \beta = - \frac{\zeta(1/2)}{\sqrt{2\pi}} \approx 0.5826 $$
으로 주어지는 것입니다. $\zeta$는 바로 리만-제타(Riemann Zeta function)이라 불리는 함수인데, 정의조차 복잡합니다. 그래도 러프하게 정의를 해보자면, $\Re(s)>1$ 인 부분에서 $$\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}$$라 정의를 합니다. 정의역을 확장시키기 위해 analytic continuation이라는 방법을 써서 $0<\Re(s)<1$에서도 정의되게끔 합니다. 이때 리만 제타 함수는
$$ \zeta(s) = \frac1{1-2^{1-s}} \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^s}$$
가 됩니다. 특히
$$ \zeta(\textstyle{\frac12}) = -1.460354$$
정도를 보입니다.
지금까지 UOC 옵션을 연속적으로(Closed Form) 또는 이산적으로(FDM) 구하는 두 방법에 대해 알아봤고, 이 두 방법 간의 차이가 이산화 여부라는 것을 설명하며 배리어 조정 이슈까지 언급하였습니다. 다음 글에서는
파생상품 가격결정 방법론의 끝판왕: MC
의 방법으로 가격을 구해보도록 하겠습니다. 끝으로 배리어 조정에 대한 논문을 첨부합니다.
'금융공학' 카테고리의 다른 글
| 배리어옵션 - UOC 옵션 #5 Binomial Tree(이항트리) (0) | 2022.08.29 |
|---|---|
| 배리어옵션 - UOC 옵션 #4 MonteCarlo Simulation (0) | 2022.08.29 |
| 배리어옵션 -UOC 옵션 #2 함축적 FDM (0) | 2022.08.25 |
| 배리어옵션 -UOC 옵션 #1 수학공식(Closed form) (0) | 2022.08.24 |
| 옵션 #8. 옵션 프리미엄 구하기 실습: Binomial Tree(with VBA) (0) | 2022.08.22 |



댓글